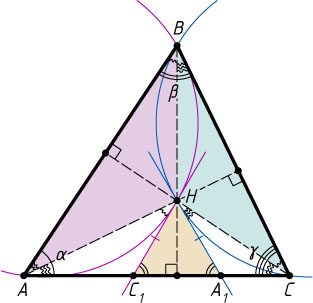
6643. Точка H
— ортоцентр треугольника ABC
. Касательные, проведённые к описанным окружностям треугольников CHB
и AHB
в точке H
, пересекают прямую AC
в точках A_{1}
и C_{1}
соответственно. Докажите, что A_{1}H=C_{1}H
.
Решение. Обозначим углы при вершинах A
, B
и C
треугольника ABC
через \alpha
, \beta
, \gamma
соответственно. Тогда
\angle CAH=90^{\circ}-\gamma,~\angle ACH=90^{\circ}-\alpha.
Из теоремы об угле между касательной и хордой (см. задачу 87) следует, что
\angle AHC_{1}=\angle ABH=90^{\circ}-\alpha,~\angle CHA_{1}=\angle CBH=90^{\circ}-\gamma.
По теореме о внешнем угле треугольника
\angle HC_{1}A_{1}=\angle AHC_{1}+\angle CAH=(90^{\circ}-\alpha)+(90^{\circ}-\gamma)=180^{\circ}-(\alpha+\gamma)=\beta,
\angle HA_{1}C_{1}=\angle CHA_{1}+\angle ACH=(90^{\circ}-\gamma)+(90^{\circ}-\alpha)=180^{\circ}-(\gamma+\alpha)=\beta.
Значит, \angle HC_{1}A_{1}=\angle HA_{1}C_{1}
. Следовательно, треугольник A_{1}HC_{1}
— равнобедренный, A_{1}H=C_{1}H
.
Автор: Швецов Д. В.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2011, VII, заочный тур, № 9, 8-9 классы
