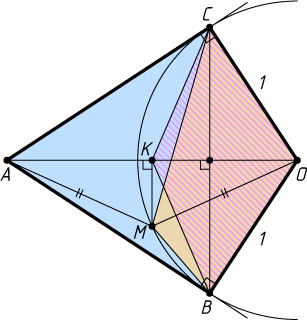
6649. Дана окружность с центром O
и радиусом 1. Из точки A
к ней проведены касательные AB
и AC
. Точка M
, лежащая на окружности, такова, что четырёхугольники OBMC
и ABMC
имеют равные площади. Найдите MA
.
Ответ. 1.
Решение. Заметим, что точка M
лежит на меньшей дуге окружности. Из точек B
и C
отрезок AO
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AO
. Центр этой окружности — середина K
отрезка AO
. Четырёхугольник ABOC
вписан в окружность и его диагонали AO
и BC
перпендикулярны (см. задачу 1180), значит, S_{OBKC}=S_{ABMC}
(см. задачу 132), а так как по условию S_{ABMC}=S_{OBMC}
, то S_{OBKC}=S_{OBMC}
. Тогда S_{\triangle BKC}=S_{\triangle BMC}
, поэтому MK\parallel BC
, а так как K
— середина AO
, то MK
— серединный перпендикуляр к отрезку AO
. Следовательно, MA=MO=1
.
Автор: Протасов В. Ю.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2011, VII, заочный тур, № 15, 9-10 классы
