6654. Высоты AA_{1}
и BB_{1}
треугольника ABC
пересекаются в точке H
. Прямая CH
пересекает полуокружность с диаметром AB
, проходящую через A_{1}
и B_{1}
, в точке D
. Отрезки AD
и BB_{1}
пересекаются в точке M
, BD
и AA_{1}
— в точке N
. Докажите, что описанные окружности треугольников B_{1}DM
и A_{1}DN
касаются.
Решение. Пусть касательные к описанным окружностям треугольников B_{1}DM
и A_{1}DN
, проведённые в общей точке D
, пересекают прямую AB
в точках Q
и P
соответственно. Из теоремы об угле между касательной и хордой следует, что
\angle ADQ=\angle MB_{1}D=\angle BB_{1}D=\angle BAD.
Аналогично \angle BDP=\angle ABD
. Точка D
лежит на окружности с диаметром AB
, поэтому \angle ADB=90^{\circ}
. Значит,
\angle ADQ+\angle BDP=\angle BAD+\angle ABD=90^{\circ}=\angle ADB.
Следовательно, касательные к обеим окружностям совпадают, т. е. окружности касаются в точке D
(см. задачу 1759).
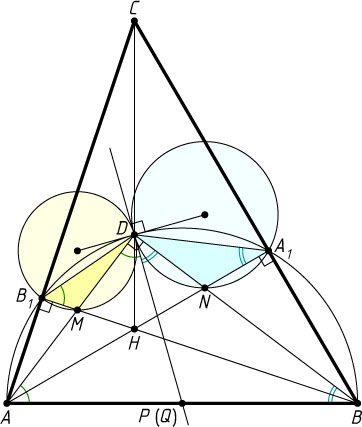
Автор: Кунгожин М. А.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2011, VII, финальный тур, № 1, 9 класс
