6657. В треугольнике ABC
проведены медианы AA_{0}
, BB_{0}
и высоты AA_{1}
, BB_{1}
. Описанные окружности треугольников CA_{0}B_{0}
и CA_{1}B_{1}
вторично пересекаются в точке M_{c}
. Аналогично определяются точки M_{a}
и M_{b}
. Докажите, что точки M_{a}
, M_{b}
, M_{c}
лежат на одной прямой, а прямые AM_{a}
, BM_{b}
, CM_{c}
параллельны.
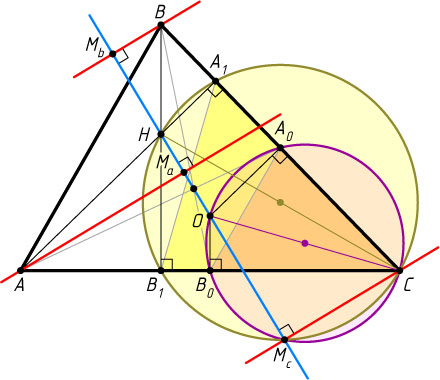
Решение. Пусть O
— центр описанной окружности треугольника ABC
, а H
— точка пересечения его высот. Поскольку
\angle CA_{0}O=\angle CB_{0}O=\angle CA_{1}H=\angle CB_{1}H=90^{\circ},
то CO
и CH
— диаметры окружностей CA_{0}B_{0}
и CA_{1}B_{1}
соответственно. Таким образом, на сторонах CH
и CO
треугольника HCO
как на диаметрах построены окружности. Тогда их точка пересечения M_{c}
, отличная от C
, лежит на прямой OH
(см. задачу 1675). Аналогично точки M_{a}
и M_{b}
также лежат на прямой OH
. Следовательно, точки M_{a}
, M_{b}
, M_{c}
лежат на одной прямой (прямой Эйлера треугольника ABC
).
Прямые AM_{a}
, BM_{b}
, CM_{c}
параллельны, так как они перпендикулярны прямой OH
.
Автор: Долгирев П. Е.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2011, VII, финальный тур, № 6, 9 класс
