6677. В треугольнике ABC
проведена высота AH
. Точки I_{b}
и I_{c}
— центры вписанных окружностей треугольников ABH
и CAH
; L
— точка касания вписанной окружности треугольника ABC
со стороной BC
. Найдите угол LI_{b}I_{c}
.
Ответ. 45^{\circ}
.
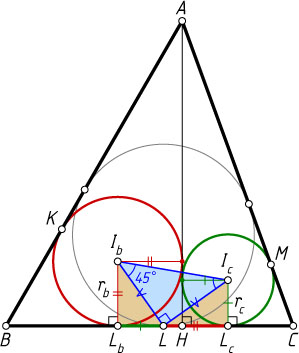
Решение. Будем считать, что AB\gt AC
. Пусть L_{b}
и L_{c}
— проекции точек I_{b}
и I_{c}
на BC
; r_{b}
и r_{c}
— радиусы окружностей, вписанных в треугольники AHB
и AHC
, а K
и M
— точки касания этих окружностей со сторонами AB
и BC
соответственно. Тогда
AB-AC=(AK+BK)-(AM+MC)=
=(AM+BL)-(AM+CL)=BL-CL.
Треугольники AHB
и AHC
прямоугольные, поэтому
r_{b}=\frac{AH+BH-AB}{2},~r_{c}=\frac{AH+CH-AC}{2}
(см. задачу 217);
r_{b}-r_{c}=\frac{BH-CH}{2}-\frac{AB-AC}{2}=\frac{BH-CH}{2}-\frac{BL-CL}{2}=
=\frac{(BH-BL)+(CL-CH)}{2}=\frac{LH+LH}{2}=LH.
Значит,
LL_{b}=HL_{b}-LH=r_{b}-(r_{b}-r_{c})=r_{c}=I_{c}L_{c}.
Аналогично LL_{c}=I_{b}L_{b}
. Прямоугольные треугольники LI_{b}L_{b}
и I_{c}LL_{c}
равны по двум катетам, поэтому LI_{b}=LI_{c}
и \angle I_{b}LI_{c}=90^{\circ}
. Значит, треугольник LI_{b}I_{c}
— равнобедренный и прямоугольный. Следовательно, \angle LI_{b}I_{c}=45^{\circ}
.
Примечание. Пусть I_{1}
, I_{2}
— центры вписанных окружностей треугольников ABD
и ACD
соответственно (D
— произвольная точка на стороне BC
), L
— точка касания вписанной окружности треугольника ABC
со стороной BC
. Тогда точки I_{1}
, L
, D
и I_{2}
лежат на одной окружности.