6684. В неравнобедренном треугольнике ABC
проведены высота из вершины A
и биссектрисы из двух других вершин. Докажите, что описанная окружность треугольника, образованного этими тремя прямыми, касается биссектрисы, проведённой из вершины A
.
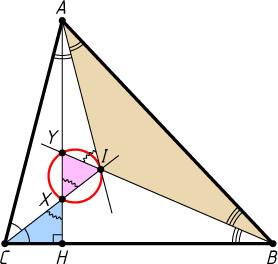
Решение. Пусть I
— точка пересечения биссектрис треугольника ABC
, а X
и Y
— точки пересечения высоты AH
с биссектрисами углов C
и B
соответственно. Пусть для определённости AB\gt AC
. Тогда точки I
и Y
лежат на отрезках BY
и AX
соответственно. По теореме о внешнем угле треугольника
\angle AIY=\frac{1}{2}\angle A+\frac{1}{2}\angle B=90^{\circ}-\frac{1}{2}\angle C=\angle CXH=\angle IXY.
Следовательно, AI
— касательная к описанной окружности треугольника XIY
(см. задачу 1735).
Автор: Рожкова М. Н.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2010, VI, финальный тур, № 1, 8 класс
Источник: Всероссийская олимпиада по геометрии. — 2010, 8 класс
