6696. Биссектрисы углов трапеции образуют при пересечении четырёхугольник с перпендикулярными диагоналями. Докажите, что трапеция равнобокая.
Решение. Пусть KLMN
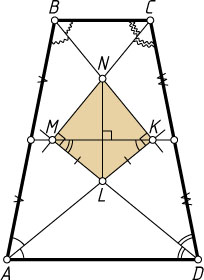
— четырёхугольник, образованный биссектрисами углов трапеции ABCD
, причём биссектрисы углов при боковой стороне AB
пересекаются в точке K
(см. рис.). Тогда \angle LKN=90^{\circ}
. Аналогично, \angle LMN=90^{\circ}
. Следовательно,
LK^{2}+KN^{2}=LN^{2}=LM^{2}+MN^{2}.
С другой стороны, из перпендикулярности диагоналей получаем, что
KL^{2}+MN^{2}=KN^{2}+LM^{2}
(см. задачу 1344). Из этих двух равенств следует, что KL=LM
, а значит, \angle LKM=\angle LMK
. Но точки K
и M
лежат на средней линии трапеции (см. задачу 1286), поэтому KM\parallel AD
. Тогда
\angle LAD=\angle LKM,~\angle ADL=\angle LMK,
поэтому
\angle BAD=2\angle LAD=2\angle ADL=\angle ADC.
Следовательно, трапеция равнобокая.
Автор: Шноль Д. Э.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2009, V, заочный тур, № 3, 8 класс
Источник: Всероссийская олимпиада по геометрии. — 2009, 8-11 классы
