6700. Задача Ферма. Внутри остроугольного треугольника найдите точку, сумма расстояний от которой до вершин минимальна.
Указание. Пусть P
— точка внутри данного остроугольного треугольника ABC
. Рассмотрите образ треугольника APB
при повороте на 60^{\circ}
вокруг точки A
и воспользуйтесь неравенством треугольника.
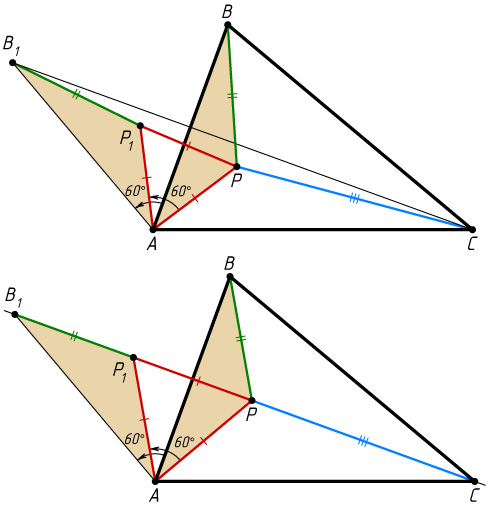
Решение. Первый способ. Пусть P
— некоторая точка внутри остроугольного треугольника ABC
. При повороте на 60^{\circ}
вокруг вершины A
треугольник ABP
переходит в равный ему треугольник AP_{1}B_{1}
, а треугольник AP_{1}P
— равносторонний (рис. 1). Поэтому
PB+PA+PC=B_{1}P_{1}+P_{1}P+PC\geqslant B_{1}C,
причём равенство достигается только в случае, когда точки P_{1}
и P
лежат на отрезке B_{1}C
. Тогда \angle APC=120^{\circ}
, т. е. сторона AC
видна из точки P
под углом 120^{\circ}
.
Аналогично докажем, что \angle APB=120^{\circ}
. Следовательно, \angle BPC=120^{\circ}
. Таким образом, каждая сторона треугольника видна из искомой точки P
под углом 120^{\circ}
. Поэтому для построения точки P
достаточно построить на двух сторонах треугольника как на хордах дуги, вмещающие углы 120^{\circ}
(см. задачу 2889).
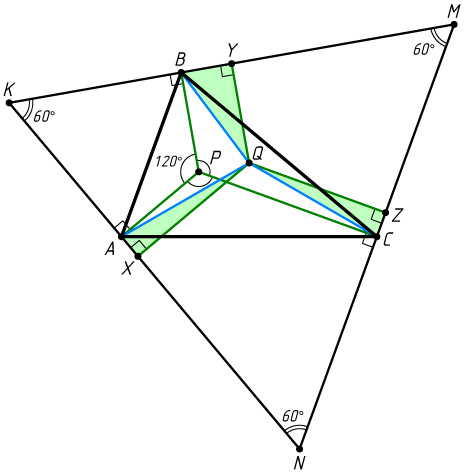
Второй способ. Пусть P
— точка, внутри треугольника ABC
, из которой все стороны видны под углом 120^{\circ}
(рис. 2). Через вершины A
, B
и C
проведём прямые, перпендикулярные отрезкам PA
, PB
и PC
. Пусть M
, N
и K
— точки пересечения этих прямых. Тогда треугольник MNK
— равносторонний.
Если Q
— произвольная точка внутри треугольника ABC
, а X
, Y
и Z
— её проекции на стороны KN
, KM
и MN
треугольника MNK
, проходящие через точки A
, B
и C
соответственно, то
PA+PB+PC=QX+QY+QZ
(каждая из этих сумм равна высоте треугольника MNK
).
Поскольку QX\leqslant QA
, QY\leqslant QB
и QZ\leqslant QC
, то
PA+PB+PC\leqslant QA+QB+QC.
Примечание. 1. Эти решения годятся и для тупоугольного треугольника, если его наибольший угол меньше 120^{\circ}
. Кроме того, по теореме косинусов квадрат суммы расстояний от этой точки P
до вершин треугольника со сторонами BC=a
, AC=b
, AB=c
, углом BAC=\alpha
и площадью S
равен
CB_{1}^{2}=AC^{2}+AB_{1}^{2}-2AC\cdot AB_{1}\cos\angle CAB_{1}=b^{2}+c^{2}-2bc\cos(60^{\circ}+\alpha)=
=b^{2}+c^{2}-bc\cos\alpha+bc\sqrt{3}\sin\alpha=b^{2}+c^{2}-\frac{1}{2}(b^{2}+c^{2}-a^{2})+2S\sqrt{3}=
=\frac{1}{2}(a^{2}+b^{2}+c^{2})+2S\sqrt{3}.
Если наибольший угол треугольника не меньше 120^{\circ}
, то искомая точка — вершина этого угла. Докажем это.
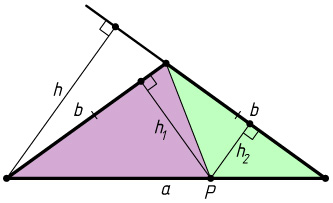
Лемма 1. Если точка лежит на основании равнобедренного треугольника, то сумма расстояний от неё до прямых, содержащих боковые стороны, равна высоте, опущенной на боковую сторону.
Доказательство. Пусть стороны треугольника равны a
, b
и b
(рис. 3), расстояния от точки P
, лежащей на основании, до прямых, содержащих боковые стороны, равны h_{1}
и h_{2}
, площадь треугольника равна S
, а высота, опущенная на боковую сторону равна h
. Тогда
S=\frac{1}{2}bh_{1}+\frac{1}{2}bh_{2}=\frac{1}{2}bh,
откуда h_{1}+h_{2}=h
. Лемма доказана.
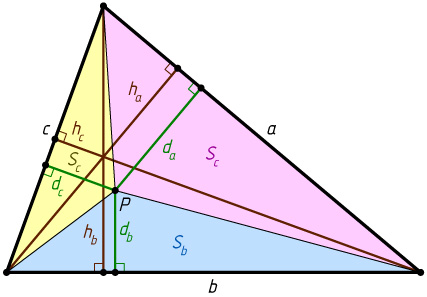
Лемма 2. Если точка P
, лежащая внутри треугольника со сторонами a
, b
и c
, удалена от прямых, содержащих стороны, на расстояния d_{a}
, d_{b}
и d_{c}
соответственно, а h_{a}
, h_{b}
и h_{c}
— соответствующие высоты треугольника, то
\frac{d_{a}}{h_{a}}+\frac{d_{b}}{h_{b}}+\frac{d_{c}}{h_{c}}=1.
Доказательство. Соединим точку P
с вершинами треугольника (рис. 4). Пусть S_{a}
, S_{b}
и S_{c}
— площади образовавшихся треугольников со сторонами a
, b
и c
соответственно. Тогда S_{a}=\frac{1}{2}ad_{a},~S_{b}=\frac{1}{2}bd_{b}
, S_{c}=\frac{1}{2}cd_{c}
. В то же время,
S=\frac{1}{2}ah_{a},~S=\frac{1}{2}bh_{b},~S=\frac{1}{2}ch_{c},
поэтому
\frac{S_{a}}{S}=\frac{d_{a}}{h_{a}},~\frac{S_{b}}{S}=\frac{d_{b}}{h_{b}},~\frac{S_{c}}{S}=\frac{d_{c}}{h_{c}}.
Сложив эти три равенства, получим, что
\frac{S_{a}}{S}+\frac{S_{b}}{S}+\frac{S_{c}}{S}=\frac{d_{a}}{h_{a}}+\frac{d_{b}}{h_{b}}+\frac{d_{c}}{h_{c}},
а так как
\frac{S_{a}}{S}+\frac{S_{b}}{S}+\frac{S_{c}}{S}=\frac{S_{a}+S_{b}+S_{c}}{S}=\frac{S}{S}=1,
то
\frac{d_{a}}{h_{a}}+\frac{d_{b}}{h_{b}}+\frac{d_{c}}{h_{c}}=1.
Лемма доказана.
Лемма 3. Если угол при вершине равнобедренного треугольника не больше 60^{\circ}
, то сумма расстояний от любой точки до прямых, содержащих стороны треугольника, не меньше высоты, опущенной на боковую сторону.
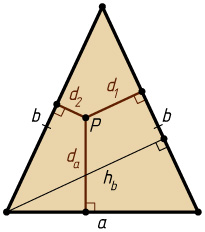
Доказательство. Пусть точка P
лежит внутри треугольника со сторонами b
, b
и a
(рис. 5), расстояния от точки P
до этих сторон равны d_{1}
, d_{2}
и d_{a}
соответственно, а высота, опущенная на боковую сторону, равна h_{b}
.
Поскольку угол при вершине равнобедренного треугольника меньше 60^{\circ}
, углы при основании больше 60^{\circ}
, поэтому угол при вершине — наименьший угол треугольника. Значит, a\leqslant b
, а поэтому h_{a}\geqslant h_{b}
. Тогда по лемме 2 имеем:
1=\frac{d_{a}}{h_{a}}+\frac{d_{1}}{h_{b}}+\frac{d_{2}}{h_{b}}\leqslant\frac{d_{a}}{h_{b}}+\frac{d_{1}}{h_{b}}+\frac{d_{2}}{h_{b}}=\frac{d_{a}+d_{1}+d_{2}}{h_{b}}.
Следовательно, d_{a}+d_{1}+d_{2}\geqslant h_{b}
.
Если точка P
лежит вне треугольника, то в равенстве \frac{d_{a}}{h_{a}}+\frac{d_{1}}{h_{b}}+\frac{d_{2}}{h_{b}}=1
одно из слагаемых нужно взять со знаком «-
», например: \frac{d_{a}}{h_{a}}-\frac{d_{1}}{h_{b}}+\frac{d_{2}}{h_{b}}=1
. Тогда \frac{d_{a}}{h_{a}}+\frac{d_{1}}{h_{b}}+\frac{d_{2}}{h_{b}}\leqslant1
. Ясно, что доказанное неравенство верно и для точки, лежащей на стороне треугольника.
Лемма доказана.
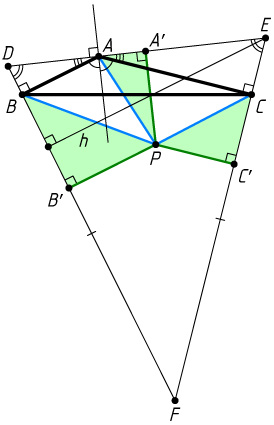
Перейдём к нашему утверждению. Пусть угол при вершине A
треугольника ABC
не меньше 120^{\circ}
(рис. 6). Через точки B
и C
проведём прямые, перпендикулярные AB
и AC
соответственно, а через точку A
— прямую перпендикулярную биссектрисе угла BAC
. Пусть две первые проведённые прямые пересекаются в точке F
, а третья пересекает их в точках соответственно D
и E
.
Треугольник DEF
равнобедренный, так как
\angle EDF=90^{\circ}-\angle DAB=90^{\circ}-\angle CAE=\angle DEF,
причём его угол при вершине F
не больше 60^{\circ}
(в четырёхугольнике ABFC
углы при вершинах B
и C
прямые, а угол при вершине A
не меньше 120^{\circ}
).
Из произвольной точки P
, отличной от A
, опустим перпендикуляры PA'
, PB'
и PC'
на прямые DE
, DF
и EF
соответственно. Пусть h
— высота равнобедренного треугольника DEF
, опущенная на боковую сторону. Тогда h=AB+AC
(лемма 1), а PA'+PB'+PC'\geqslant h
(лемма 3). Поскольку
PA\geqslant PA',~PB\geqslant PB',~PC\geqslant PC',
то
PA+PB+PC\geqslant PA'+PB'+PC'\geqslant AB+AC.
Что и требовалось доказать.
2. См. также статью Л.Радзивиловского «Ещё раз о точке Торричелли», Квант, 2014, N3, с.38-42.
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 145, с. 53
Источник: Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — с. 40
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 18.21(а), с. 70
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 11.21, с. 284
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 18.22(а), с. 375
Источник: Факультативный курс по математике: Учебное пособие для 7—9 кл. средней школы / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — с. 98
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 666, с. 83
Источник: Болтянский В. Г., Яглом И. М. Преобразования. Векторы. — М.: Просвещение, 1964. — № 223, с. 95
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 145-150
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — задача 3, с. 111