6718. Пусть ABC
— остроугольный треугольник, CC_{1}
— его биссектриса, O
— центр описанной окружности. Точка пересечения прямой OC_{1}
с перпендикуляром из C
на AB
лежит на описанной окружности треугольника AOB
. Найдите угол C
.
Ответ. 60^{\circ}
.
Решение. Заметим, что AC\ne BC
, так как иначе прямая OC_{1}
совпадает с указанным в условии перпендикуляром.
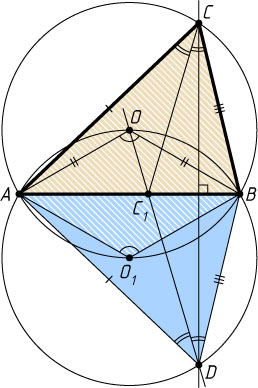
Пусть D
— точка пересечения OC_{1}
с перпендикуляром, опущенном из точки C
на прямую AB
. Поскольку точка D
лежит на описанной окружности треугольника AOB
и AO=OB
, то \angle ADC_{1}=\angle BDC_{1}
. Значит,
\frac{AD}{BD}=\frac{AC_{1}}{BC_{1}}=\frac{AC}{BC}
(см. задачу 1509), откуда 2AD\cdot BC=2AC\cdot BD
. С другой стороны, так как CD\perp AB
, то
AC^{2}+BD^{2}=AD^{2}+BC^{2}
(см. задачу 1344). Сложив эти равенства, получим, что (AC+BD)^{2}=(AD+BC)^{2}
. Значит, AC+BD=AD+BC
, а так как AC\cdot BD=AD\cdot BC
и AC\ne BC
, то AC=AD
и BD=BC
. Тогда точка D
симметрична вершине C
относительно прямой AB
, треугольник ABC
симметричен треугольнику ABD
, а описанная окружность треугольника ABC
и её центр O
симметричны описанной окружности треугольника ABD
и её центру O_{1}
. Поскольку точка O
— середина меньшей дуги AB
описанной окружности треугольника ABC
, то O_{1}
— середина симметричной ей меньшей дуги AB
описанной окружности треугольника ADC
. Четырёхугольник AO_{1}BC
— вписанный, поэтому
2\angle C=\angle AOB=\angle AO_{1}B=180^{\circ}-\angle C.
Отсюда находим, что \angle C=60^{\circ}
.
Автор: Ивлев Ф. А.
Источник: Всероссийская олимпиада по геометрии. — 2009, 9 класс
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2009, V, заочный тур, № 10, 9 класс
