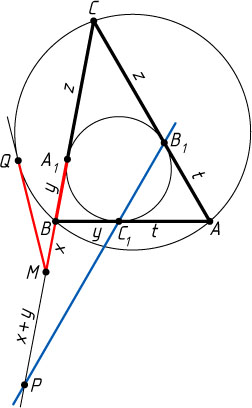
6774. Около треугольника ABC
описана окружность и в него же вписана окружность, которая касается сторон BC
, AC
и AB
в точках A_{1}
, B_{1}
и C_{1}
соответственно. Прямая B_{1}C_{1}
пересекает прямую BC
в точке P
, а точка M
— середина отрезка PA_{1}
. Докажите, что отрезки касательных, проведённых из точки M
к вписанной и описанной окружности, равны.
Решение. Пусть AB\lt AC
, а прямая, проходящая через точку M
, касается описанной окружности треугольника ABC
в точке Q
. По теореме о касательной и секущей MQ^{2}=MB\cdot MC
, поэтому достаточно доказать, что MA_{1}^{2}=MB\cdot MC
.
Обозначим MB=x
, BA_{1}=y
, CA_{1}=CB_{1}=z
, AB_{1}=AC_{1}=t
. Тогда
MA_{1}=x+y,~MC=x+y+z,~BP=2x+y,~PC=2x+2y+z,
поэтому равенство MA_{1}^{2}=MB\cdot MC
равносильно равенству (x+y)^{2}=x(x+y+z)
, или xz=y(x+y)
.
По теореме Менелая
\frac{AC_{1}}{C_{1}B}\cdot\frac{BP}{PC}\cdot\frac{CB_{1}}{B_{1}A}=1,
(см. задачу 1622), или
\frac{t}{y}\cdot\frac{2x+y}{2x+2y+z}\cdot\frac{z}{t}=1,
откуда zx=y(x+y)
. Что и требовалось доказать.
Автор: Протасов В. Ю.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2006, II, заочный тур, № 15
