6785. Дан треугольник ABC
. Проведены высота AH
и медиана CM
. Обозначим их точку пересечения через P
. Высота, проведённая из вершины B
треугольника, пересекается с перпендикуляром, опущенным из точки H
на прямую CM
, в точке Q
. Докажите, что прямые CQ
и BP
перпендикулярны.
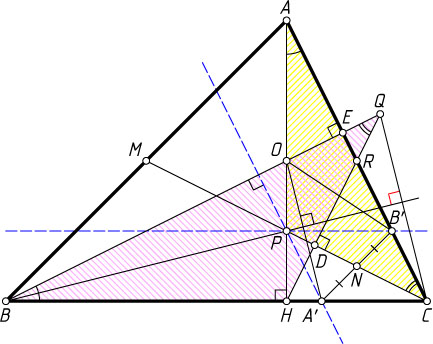
Решение. Через точку P
проведём прямые, параллельные BC
и AC
. Пусть A'
и B'
— точки пересечения этих прямых со сторонами BC
и AC
соответственно. Тогда CA'PB'
— параллелограмм. Его диагональ CP
проходит через середину N
диагонали A'B'
. Следовательно, A'B'\parallel AB
(см. задачу 6784), поэтому \frac{BA'}{A'C}=\frac{AB'}{B'C}
.
Пусть прямая HQ
пересекает медиану CM
и сторону AC
в точках D
и R
соответственно, а прямая BQ
пересекает сторону AC
в точке E
. Тогда BE
— высота треугольника ABC
, а точка O
пересечения AH
и BE
— ортоцентр треугольника ABC
.
Треугольники AHC
, BEC
, CDR
и QER
— прямоугольные, поэтому
\angle CAP=\angle CAH=\angle CBE=\angle CBQ,
\angle ACP=\angle RCD=\angle RQE=\angle HQB.
Значит, треугольник APB'
подобен треугольнику BHO
, а треугольник APC
— треугольнику BHQ
, поэтому \frac{BO}{OQ}=\frac{AB'}{B'C}=\frac{BA'}{A'C}
. Тогда из теоремы о пропорциональных отрезках следует, что A'O\parallel CQ
.
Поскольку PA'\parallel AC
и BO\perp AC
, то высота треугольника BPA'
, проведённая из вершины B
, лежит на прямой BO
, а так как PH\perp BA'
, то O
— ортоцентр треугольника BPA'
. Значит, A'O\perp BP
. Следовательно, CQ\perp BP
.
Автор: Ивлев Ф. А.
Источник: Московская математическая олимпиада. — 2015, LXXVIII, 10 класс
