6823. Точки M
и N
— середины сторон соответственно AB
и AC
треугольника ABC
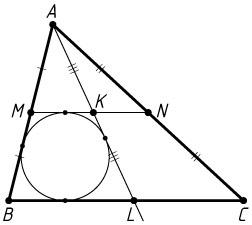
. Прямая, проходящая через вершину A
, пересекает отрезки MN
и BC
в точках K
и L
соответственно, причём в четырёхугольник BMKL
можно вписать окружность.
а) Докажите, что периметр треугольника AMK
вдвое больше отрезка BL
.
б) Найдите AL
, если AB=12
, BC=16
, AC=20
.
Ответ. 15.
Решение. а) Пусть периметр треугольника AMK
равен P
. Отрезок MK
— средняя линия треугольника ABL
, поэтому MK=\frac{1}{2}BL
. В четырёхугольник BMKL
можно вписать окружность, значит,
BM+KL=BL+MK=BL+\frac{1}{2}BL=\frac{3}{2}BL,
или
P-\frac{1}{2}BL=P-MK=AM+AK=BM+KL=\frac{3}{2}BL.
Следовательно, P=2BL
.
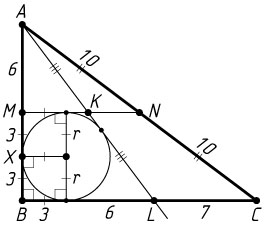
б) Треугольник ABC
прямоугольный с прямым углом при вершине B
. Пусть r
— радиус вписанной окружности четырёхугольника BMKL
(прямоугольной трапеции с основаниями BL
и MK
). Тогда r=\frac{1}{4}AB=3
.
Пусть эта окружность касается стороны BM
в точке X
. Тогда
MX=r=3,~AX=AM+MX=6+3=9,~
а так как отрезок AX
равен полупериметру треугольника AMK
(см. задачу 4805), то по доказанному BL=AX=9
. Следовательно,
AL=\sqrt{AB^{2}+BL^{2}}=\sqrt{12^{2}+9^{2}}=15.
