6851. Высоты BB_{1}
и CC_{1}
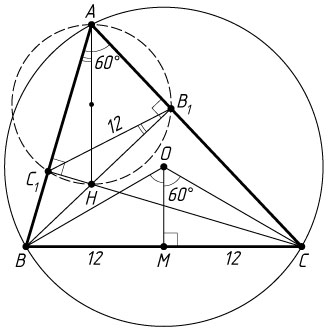
остроугольного треугольника ABC
пересекаются в точке H
.
а) Докажите, что \angle BB_{1}C_{1}=\angle BAH
.
б) Найдите расстояние от центра описанной окружности треугольника ABC
до стороны BC
, если известно, что B_{1}C_{1}=12
и \angle BAC=60^{\circ}
.
Ответ. 4\sqrt{3}
.
Решение. а) Из точек B_{1}
и C_{1}
отрезок AH
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AH
. Вписанные в эту окружность углы HAC_{1}
и HB_{1}C_{1}
опираются на одну и ту же дугу, следовательно,
\angle BB_{1}C_{1}=\angle HB_{1}C_{1}=\angle HAC_{1}=\angle BAH.
Что и требовалось доказать.
б) Треугольник AB_{1}C_{1}
подобен треугольнику ABC
с коэффициентом \cos\angle BAC=\cos60^{\circ}=\frac{1}{2}
(см. задачу 19). Следовательно, BC=2B_{1}C_{1}=24
.
Пусть O
— центр описанной окружности треугольника ABC
, M
— середина стороны BC
. Тогда расстояние от точки O
до стороны BC
равно длине отрезка OM
(см. задачу 1677), а так как вписанный угол BAC
вдвое меньше центрального угла BOC
, то
\angle MOC=\frac{1}{2}\angle BOC=\angle BAC=60^{\circ}.
Из прямоугольного треугольника COM
находим, что
OM=CM\ctg\frac{1}{2}\angle BOC=\frac{1}{2}BC\ctg60^{\circ}=12\cdot\frac{\sqrt{3}}{3}=4\sqrt{3}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2015
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 15.28.1, с. 163
