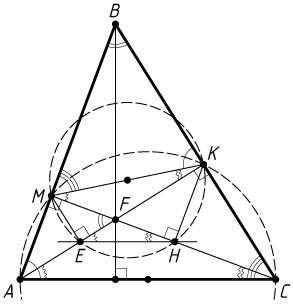
6861. В остроугольном треугольнике ABC
провели высоты AK
и CM
, а из точек M
и K
опустили перпендикуляры ME
и KH
на прямые AK
и CM
соответственно.
а) Докажите, что прямые EH
и AC
параллельны.
б) Найдите отношение EH:AC
, если \angle ABC=30^{\circ}
.
Ответ. 3:4
.
Указание. См. задачу 19.
Решение. а) Из точек M
и K
отрезок AC
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AC
. Вписанные в эту окружность углы ACM
и AKM
опираются на одну и ту же дугу, поэтому
\angle ACM=\angle AKM.
Из точек E
и H
отрезок MK
виден под прямым углом, значит, эти точки лежат на окружности с диаметром MK
. Вписанные в эту окружность углы MHE
и MKE
опираются на одну и ту же дугу, поэтому
\angle EHM=\angle EKM=\angle AKM.
Значит, \angle EHM=\angle ACM
. Следовательно, EH\parallel AC
.
б) Треугольник BKM
подобен треугольнику BAC
по двум углам, причём коэффициент подобия равен
\frac{BK}{AB}=\cos\angle ABC=\cos30^{\circ}=\frac{\sqrt{3}}{2}.
Значит,
MK=AC\cdot\frac{\sqrt{3}}{2}=\frac{AC\sqrt{3}}{2}.
Пусть F
— точка пересечения высот треугольника ABC
. Тогда
\angle EFM=\angle AFM=90^{\circ}-\angle BAK=\angle ABC=30^{\circ}.
Треугольник EFH
подобен треугольнику MFK
по двум углам, причём коэффициент подобия равен
\frac{EF}{MF}=\cos\angle EFM=\cos30^{\circ}=\frac{\sqrt{3}}{2}.
Значит,
EH=\frac{MK\sqrt{3}}{2}=\frac{3}{4}AC.
Следовательно, \frac{EH}{AC}=\frac{3}{4}
.
Источник: ЕГЭ. — 2016
