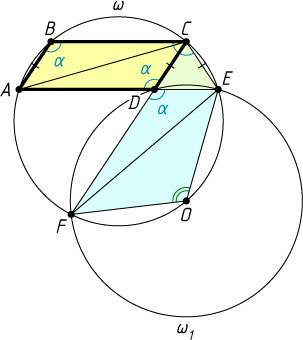
6894. Дан параллелограмм ABCD
, в котором угол ABC
тупой. Прямая AD
пересекает второй раз окружность \omega
, описанную вокруг треугольника ABC
, в точке E
. Прямая CD
пересекает второй раз окружность \omega
в точке F
. Докажите, что центр описанной окружности треугольника DEF
лежит на окружности \omega
.
Решение. Пусть
\angle ABC=\angle ADC=\angle EDF=\alpha\gt90^{\circ}.
Трапеция ABCE
вписана в окружность \omega
, поэтому она равнобедренная (см. задачу 5003). Значит,
\angle ECF=\angle BCE-\angle BCD=\alpha-(180^{\circ}-\alpha)=2\alpha-180^{\circ}.
Пусть O
— центр окружности \omega_{1}
, описанной вокруг треугольника DEF
. Точка O
лежит внутри угла EDF
, поскольку \angle EDF\gt90^{\circ}
, причём точки D
и O
лежат по разные стороны от прямой EF
. В окружности \omega_{1}
вписанный угол EDF
опирается на дугу, равную 360^{\circ}-2\alpha
, значит, центральный угол EOF
этой окружности равен 360^{\circ}-2\alpha
. Тогда
\angle EOF+\angle ECF=(360^{\circ}-2\alpha)+(2\alpha-180^{\circ})=180^{\circ},
поэтому четырёхугольник CEOF
вписанный. Следовательно, точка O
лежит на окружности \omega
.
Автор: Емельянова Т. Л.
Источник: Всероссийская олимпиада школьников. — 2008-2009, XXXV, региональный этап, 9 класс
Источник: Журнал «Квант». — 2009, № 2, с. 54
