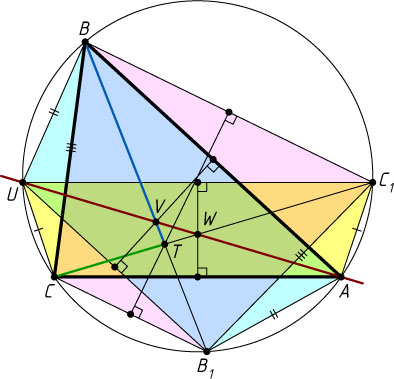
6911. В треугольнике ABC
угол A
наименьший. Пусть U
— точка на той дуге описанной около треугольника окружности, которая не содержит точку A
. Серединные перпендикуляры к отрезкам AB
и AC
пересекают прямую AU
в точках V
и W
соответственно. Прямые BV
и CW
пересекаются в точке T
. Докажите, что AU=TB+TC
.
Указание. Проведите хорды UC_{1}\parallel AC
и UB_{1}\parallel AB
.
Решение. Проведём хорды UC_{1}\parallel AC
и UB_{1}\parallel AB
. Дуги, заключённые между параллельными хордами, равны (см. задачу 1678), значит, равны дуги AC_{1}
и UC
, не содержащие точек C
и B
соответственно. При этом точка C_{1}
лежит на дуге AB
, не содержащей точки C
, а точка B_{1}
— на дуге AC
, не содержащей точки B
(угол A
— наименьший угол треугольника, поэтому \smile BC\lt\smile AB
и \smile BC\lt\smile AC
).
Вписанная трапеция ACUC_{1}
равнобедренная, поэтому она симметрична относительно серединного перпендикуляра к её основанию CB_{1}
. Значит, точка пересечения диагоналей AU
и CC_{1}
совпадает с W
и AU=CC_{1}
. Аналогично, точка пересечения диагоналей равнобедренной трапеции ABUB_{1}
совпадает с V
.
Поскольку
\smile B_{1}AC_{1}=\smile B_{1}A+\smile AC_{1}=\smile UB+\smile UC=\smile BUC,
хорды BC_{1}
и CB_{1}
параллельны. Значит, BC_{1}B_{1}C
— также равнобедренная трапеция с диагоналями BB_{1}
и CC_{1}
, пересекающимися в точке T
. Следовательно,
TB+TC=TC_{1}+TC=CC_{1}=AU.
Источник: Международная математическая олимпиада. — 1997, LXIII, Великобритания
Источник: Журнал «Квант». — 1998, № 1, с. 21, М1626; 1998, № 4, с. 27, М1626
Источник: Задачник «Кванта». — М1626
Источник: Агаханов Н. Х., Кожевников П. А., Терёшин Д. А. Математика. Международные олимпиады. — М.: Просвещение, 2010. — № 97.1, с. 33
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.40, с. 35
