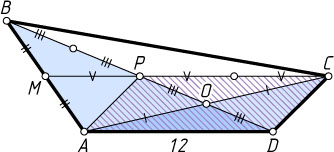
6920. В выпуклом четырёхугольнике ABCD
площади треугольников ABD
и BCD
равны, а площадь треугольника ACD
равна половине площади треугольника ABD
. Точка M
— середина стороны AB
. Найдите CM
, если известно, что AD=12
.
Ответ. 18
.
Решение. Диагональ BD
делит площадь четырёхугольника ABCD
пополам, значит, она делит пополам и его диагональ AC
(см. задачу 3157). Пусть диагонали четырёхугольника пересекаются в точке O
. Тогда BO
и DO
— медианы треугольников ABC
и ACD
.
Положим S_{\triangle ACD}=2x
. Тогда
S_{\triangle AOD}=x,~S_{\triangle ABD}=2S_{\triangle ACD}=4x,~S_{\triangle AOB}=4x-x=3x,
значит,
\frac{BO}{OD}=\frac{S_{\triangle AOB}}{S_{\triangle AOD}}=\frac{3x}{x}=3.
Пусть P
— точка пересечения CM
и BD
. Тогда P
— точка пересечения медиан треугольника ABC
, поэтому OP=\frac{1}{3}BO=OD
. Диагонали AC
и DP
четырёхугольника ADCP
точкой пересечения делятся пополам, значит, это параллелограмм. Следовательно,
CM=\frac{3}{2}CP=\frac{3}{2}AD=\frac{3}{2}\cdot12=18.
Источник: Математическая олимпиада МГУ «Ломоносов». — 2014-2015, заключительный этап, 9 класс; тренировочная задача, № 5, вариант 4, 10-11 классы
Источник: Бегунц А. В., Бородин П. А. и др. Олимпиада школьников «Ломоносов» по математике (2005—2018). — М.: МЦНМО, 2019. — с. 123
