6922. В окружности радиуса R
проведены хорды AB
и AC
. На хорде AB
или на её продолжении за точку B
взята точка M
, расстояние от которой до прямой AC
равно AC
. Аналогично, на хорде AC
или на её продолжении за точку C
взята точка N
, расстояние от которой до прямой AB
равно AB
. Найдите MN
.
Ответ. 2R
.
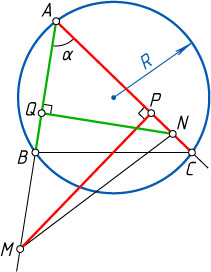
Решение. Пусть P
и Q
— проекции точек M
и N
на прямые AC
и AB
соответственно. Обозначим \angle BAC=\alpha
. Из прямоугольных треугольников AMP
и ANQ
получаем, что
AM=\frac{MP}{\sin\alpha}=\frac{AC}{\sin\alpha},~AN=\frac{NQ}{\sin\alpha}=\frac{AB}{\sin\alpha}.
Значит, \frac{AM}{AN}=\frac{AC}{AB}
. Тогда треугольник ANM
подобен треугольнику ABC
с коэффициентом \frac{1}{\sin\alpha}
. Следовательно, по теореме синусов
MN=\frac{BC}{\sin\alpha}=2R
(см. задачу 23).
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 265, с. 30
