6930. В трапеции ABCD
основания AD
и BC
равны соответственно 36 и 12, а сумма углов при основании AD
равна 90^{\circ}
. Найдите радиус окружности, проходящей через точки A
и B
и касающейся прямой CD
, если AB=13
.
Ответ. 13.
Решение. Пусть прямые AB
и CD
пересекаются в точке P
. Тогда \angle APD=90^{\circ}
, а треугольник BPC
подобен треугольнику PAD
с коэффициентом \frac{BC}{AD}=\frac{1}{3}
. Значит, PB=\frac{1}{2}AB=\frac{13}{2}
.
Пусть окружность с центром O
радиуса R
, проходящая через точки A
и B
, касается прямой CD
в точке M
.
Первый способ. По теореме о касательной и секущей (см. задачу 93)
PM^{2}=PB\cdot PA=\frac{13}{2}\cdot\frac{3}{2}\cdot13=\frac{3}{4}\cdot13^{2}.
Значит, PM=\frac{13\sqrt{3}}{2}
. Поскольку прямые OM
и BP
перпендикулярны одной и той же прямой CD
, они параллельны. Пусть H
— основание перпендикуляра, опущенного из точки B
на радиус OM
. Тогда
OH=OM-HM=OM-BP=R-\frac{13}{2},~BH=PM=\frac{13\sqrt{3}}{2}.
По теореме Пифагора OH^{2}+BH^{2}=OB^{2}
, или
\left(R-\frac{13}{2}\right)^{2}+\left(\frac{13\sqrt{3}}{2}\right)^{2}=R^{2},
откуда находим, что R=13
.
Второй способ. Опустим перпендикуляр OQ
на хорду AB
окружности, тогда Q
— середина AB
, QB=\frac{13}{2}
. Четырёхугольник QPMO
— прямоугольник. Следовательно,
R=OM=QP=QB+BP=\frac{13}{2}+\frac{13}{2}=13.
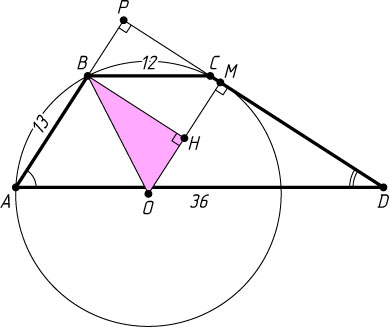
Источник: Диагностические и тренировочные задачи ОГЭ (ГИА). — 2016, задача 26
