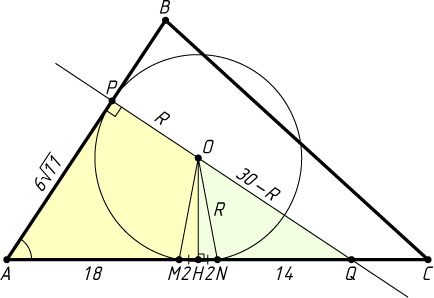
6932. Точки M
и N
лежат на стороне AC
треугольника ABC
на расстояниях 18 и 22 от вершины A
. Найдите радиус окружности, проходящей через M
и N
и касающейся луча AB
, если \cos\angle BAC=\frac{\sqrt{11}}{6}
.
Ответ. 10,8.
Решение. Пусть O
— центр окружности радиуса R
, проходящей через точки M
и N
и касающейся луча AB
в точке P
, Q
— точка пересечения прямых PO
и AC
.
По теореме о касательной и секущей (см. задачу 93)
AP=\sqrt{AM\cdot AN}=\sqrt{18\cdot22}=6\sqrt{11}.
Из прямоугольного треугольника APQ
находим, что
AQ=\frac{AP}{\cos\angle BAC}=\frac{6\sqrt{11}}{\frac{\sqrt{11}}{6}}=36,
PQ=\sqrt{AQ^{2}-AP^{2}}=\sqrt{36^{2}-36\cdot11}=6\sqrt{25}=30.
Пусть AM=18
, AN=22
, а H
— основание перпендикуляра, опущенного из точки O
на хорду MN
. Тогда H
— середина MN
, поэтому
MH=\frac{1}{2}(AN-AM)=2,~AH=AM+MH=20,
QH=AQ-AH=36-20=16.
Прямоугольные треугольники QOH
и QAP
подобны, поэтому \frac{QH}{OQ}=\frac{PQ}{AQ}
, или \frac{16}{OQ}=\frac{30}{36}
, откуда OQ=\frac{96}{5}
. Следовательно,
R=OP=PQ-OQ=30-\frac{96}{5}=\frac{54}{5}=10{,}8.
Источник: Диагностические и тренировочные задачи ОГЭ (ГИА). — 2016, задача 26
