6935. В треугольнике ABC
биссектриса BE
и медиана AD
перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника.
Ответ. 52\sqrt{13}
, 104\sqrt{13}
, 165\sqrt{5}
.
Решение. Пусть биссектриса BE
и медиана AD
пересекаются в точке O
. Биссектриса BO
треугольника ABD
является его высотой, значит, этот треугольник равнобедренный. Тогда OD=OA=104
и CD=BD=AB
. По свойству биссектрисы треугольника AE:EC=AB:BC=1:2
(см. задачу 1509).
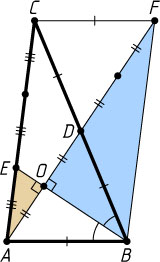
Достроим треугольник ABC
до параллелограмма ABFC
. Тогда BF=AC=3AE
, а так как треугольники AOE
и FOB
подобны, то BO:OE=BF:AE=3
. Значит,
BO=\frac{3}{4}BE=156,~OE=\frac{1}{4}BE=52.
По теореме Пифагора
BD=\sqrt{BO^{2}+OD^{2}}=\sqrt{156^{2}+104^{2}}=52\sqrt{9+4}=52\sqrt{13},
AE=\sqrt{OE^{2}+OA^{2}}=\sqrt{52^{2}+104^{2}}=52\sqrt{1+4}=52\sqrt{5}.
Следовательно,
AB=BD=52\sqrt{13},~BC=2BD=104\sqrt{13},~AC=3AE=156\sqrt{5}.
