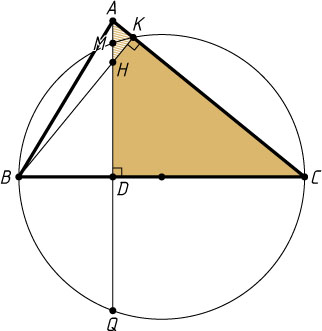
6939. На стороне BC
остроугольного треугольника ABC
(AB\ne AC
) как на диаметре построена полуокружность, пересекающая высоту AD
в точке M
, AD=49
, MD=42
, H
— точка пересечения высот треугольника ABC
. Найдите AH
.
Ответ. 13.
Решение. Пусть окружность с диаметром BC
пересекается с прямой AC
в точке K
. Поскольку BK
— высота остроугольного треугольника ABC
, точка K
лежит на стороне AC
. Продолжим высоту AD
за точку D
до пересечения с окружностью в точке Q
. Тогда DQ=MD=42
. По следствию из теоремы о касательной и секущей (см. задачу 2636)
AK\cdot AC=AM\cdot AQ=(49-42)(49+42)=49^{2}-42^{2}=7\cdot91.
Из подобия прямоугольных треугольников AKH
и ADC
следует, что \frac{AK}{AH}=\frac{AD}{AC}
, откуда
AK\cdot AC=AH\cdot AD=49AH.
Таким образом, получаем уравнение 49AH=7\cdot91
, из которого находим, что AH=13
.
Источник: Диагностические и тренировочные задачи ОГЭ (ГИА). — 2016, задача 26
