6949. Прямая проходит через центр квадрата со стороной 1. Найдите сумму квадратов расстояний от всех вершин квадрата до этой прямой.
Ответ. 1.
Указание. Рассмотрите поворот на 90^{\circ}
вокруг центра квадрата (или примените метод координат).
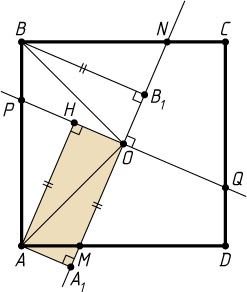
Решение. Первый способ. Пусть O
— центр квадрата ABCD
со стороной 1, прямая, проходящая через точку O
, пересекает стороны AD
и BC
в точках соответственно M
и N
, не совпадающих с вершинами и серединами сторон квадрата, A_{1}
и B_{1}
— проекции вершин соответственно A
и B
на эту прямую.
Через точку O
проведём прямую, перпендикулярную MN
. Пусть она пересекает стороны AB
и CD
квадрата ABCD
в точках P
и Q
соответственно, а H
— проекция точки A
на прямую PQ
.
Рассмотрим поворот вокруг точки O
, при котором вершина A
переходит в B
. Прямая PQ
при этом перейдёт в прямую NM
, прямая AB
— в прямую BC
. Значит, точка P
перейдёт в N
, отрезок AP
— в отрезок BN
, а перпендикуляр AH
к прямой PQ
— в перпендикуляр BB_{1}
к прямой MN
. Следовательно, AH=BB_{1}
.
Отрезок OA
— диагональ прямоугольника AHOA_{1}
, значит,
AA_{1}^{2}+BB_{1}^{2}=AA_{1}^{2}+AH^{2}=OA^{2}=\left(\frac{\sqrt{2}}{2}\right)^{2}=\frac{1}{2},
а так как расстояния от вершин C
и D
до прямой MN
равны расстояниям до этой прямой от вершин соответственно A
и B
, то искомая сумма квадратов расстояний от всех вершин квадрата до этой прямой равна 1.
Если же прямая MN
проходит через вершины или середины сторон квадрата, искомая сумма квадратов очевидно также равна 1.
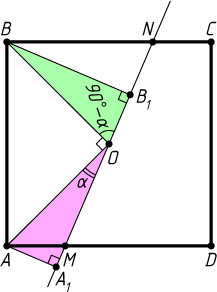
Второй способ. Пусть O
— центр квадрата ABCD
со стороной 1, прямая, проходящая через точку O
, пересекает стороны AD
и BC
в точках соответственно M
и N
, не совпадающих с вершинами и серединами сторон квадрата, A_{1}
и B_{1}
— проекции вершин соответственно A
и B
на эту прямую.
Пусть \angle AOM=\alpha\lt90^{\circ}
. Тогда \angle BON=90^{\circ}-\alpha
. Из прямоугольных треугольников AA_{1}O
и BB_{1}O
находим, что
AA_{1}=OA\sin\alpha=\frac{\sqrt{2}}{2}\sin\alpha,~AB_{1}=OA\sin(90^{\circ}-\alpha)=\frac{\sqrt{2}}{2}\cos\alpha.
Значит,
AA_{1}^{2}+BB_{1}^{2}=\frac{1}{2}\sin^{2}\alpha+\frac{1}{2}\cos^{2}\alpha=\frac{1}{2}(\sin^{2}\alpha+\cos^{2}\alpha)=\frac{1}{2}.
Аналогично для суммы квадратов расстояний от остальных вершин квадратов до прямой MN
. Следовательно, сумма квадратов расстояний от всех вершин квадрата до прямой MN
равна 1.
Если же прямая MN
проходит через вершины или середины сторон квадрата, искомая сумма квадратов очевидно также равна 1.
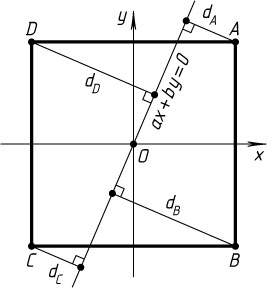
Третий способ. Пусть O
— центр квадрата ABCD
со стороной 1. Рассмотрим прямоугольную систему координат с началом в точке O
. Ось Ox
направим по лучу, сонаправленному с лучом DA
, а ось Oy
— по лучу, сонаправленному с лучом BA
. Тогда вершины квадрата суть A\left(\frac{1}{2};\frac{1}{2}\right)
, B\left(-\frac{1}{2};\frac{1}{2}\right)
, C\left(-\frac{1}{2};-\frac{1}{2}\right)
, D\left(\frac{1}{2};-\frac{1}{2}\right)
, а прямая задаётся уравнением ax+by=0
. Квадраты расстояний от вершин A
, B
, C
и D
до прямой соответственно равны (см. задачу 4249)
d_{A}^{2}=\left(\frac{\left|\frac{1}{2}a+\frac{1}{2}b\right|}{\sqrt{a^{2}+b^{2}}}\right)^{2}=\frac{a^{2}+2ab+b^{2}}{4(a^{2}+b^{2})},
d_{B}^{2}=\left(\frac{\left|-\frac{1}{2}a+\frac{1}{2}b\right|}{\sqrt{a^{2}+b^{2}}}\right)^{2}=\frac{a^{2}-2ab+b^{2}}{4(a^{2}+b^{2})},
d_{C}^{2}=\left(\frac{\left|-\frac{1}{2}a-\frac{1}{2}b\right|}{\sqrt{a^{2}+b^{2}}}\right)^{2}=\frac{a^{2}+2ab+b^{2}}{4(a^{2}+b^{2})},
d_{D}^{2}=\left(\frac{\left|\frac{1}{2}a-\frac{1}{2}b\right|}{\sqrt{a^{2}+b^{2}}}\right)^{2}=\frac{a^{2}-2ab+b^{2}}{4(a^{2}+b^{2})},
Следовательно,
d_{A}^{2}+d_{B}^{2}+d_{C}^{2}+d_{D}^{2}=
=\frac{1}{4}\left(\frac{a^{2}+2ab+b^{2}}{a^{2}+b^{2}}+\frac{a^{2}-2ab+b^{2}}{a^{2}+b^{2}}+\frac{a^{2}+2ab+b^{2}}{a^{2}+b^{2}}+\frac{a^{2}-2ab+b^{2}}{a^{2}+b^{2}}\right)=
=\frac{a^{2}+b^{2}}{a^{2}+b^{2}}=1.