6958. Один из двух отрезков, соединяющих середины противоположных сторон четырёхугольника, делит его площадь пополам, а другой — в отношении 11:17
.
а) Докажите, что данный четырёхугольник — трапеция.
б) Найдите отношение оснований этой трапеции.
Ответ. 2:5
.
Решение. а) Пусть M
и N
— середины сторон соответственно AD
и BC
четырёхугольника ABCD
. Отрезок NM
— медиана треугольника AND
, поэтому S_{\triangle ANM}=S_{\triangle DNM}
(см. задачу 3001). Тогда
S_{\triangle ABN}=S_{ABNM}-S_{\triangle ANM}=S_{CDMN}-S_{\triangle DNM}=S_{\triangle DCN}.
Треугольники ABN
и DCN
с равными сторонами BN
и CN
равновелики, значит, их высоты AP
и DQ
, опущенные на эти стороны, равны. Следовательно, BC\parallel AD
, т. е. четырёхугольник ABCD
— трапеция и параллелограмм.
Пусть K
и L
— середины сторон AB
и CD
соответственно. Предположим, что AB\parallel CD
. Тогда отрезок KL
разбивает параллелограмм на две равновеликие части, что противоречит условию задачи. Таким образом, четырёхугольник ABCD
— трапеция с основаниями AD
и BC
.
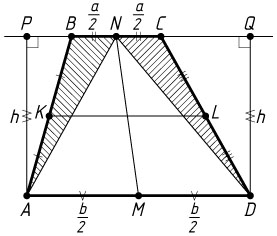
б) Пусть высота трапеции равна h
, BC=a
, AD=b
, a\lt b
. Тогда KL=\frac{a+b}{2}
, так как KL
— средняя линия трапеции. Поэтому
S_{BCLK}=\frac{a+\frac{a+b}{2}}{2}\cdot\frac{h}{2}=\frac{(3a+b)h}{8},~S_{AKLD}=\frac{b+\frac{a+b}{2}}{2}\cdot\frac{h}{2}=\frac{(a+3b)h}{8},
а так как \frac{S_{BCLK}}{S_{AKLD}}=\frac{11}{17}
, то \frac{3a+b}{a+3b}=\frac{11}{17}
. Отсюда находим, что \frac{a}{b}=\frac{2}{5}
.
Источник: ЕГЭ. — 2016
