6961. В трапеции ABCD
точка E
— середина основания AD
, точка M
— середина боковой стороны AB
. Отрезки CE
и DM
пересекаются в точке O
.
а) Докажите, что площади четырёхугольника AMOE
и треугольника COD
равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE
, если BC=3
, AD=4
.
Ответ. \frac{2}{9}
.
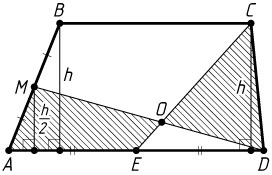
Решение. а) Пусть высота трапеции равна h
. Тогда высота треугольника AMD
равна \frac{h}{2}
. Значит,
S_{\triangle CED}=\frac{1}{2}DE\cdot h=\frac{1}{4}AD\cdot h,
S_{\triangle AMD}=\frac{1}{2}AD\cdot\frac{h}{2}=\frac{1}{4}AD\cdot h.
Следовательно, треугольники CED
и AMD
равновелики, а так как треугольник DOE
— их общая часть, то четырёхугольник AMOE
и треугольник COD
также равновелики.
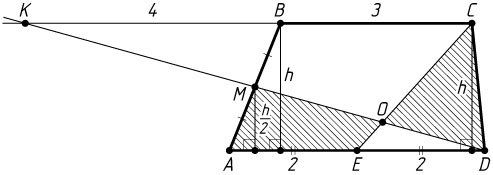
б) Пусть прямые DM
и BC
пересекаются в точке K
. Треугольники BMC
и AMD
равны по стороне и двум прилежащим к ней углам, поэтому
BK=AD=4,~CK=BC+BK=3+4=7.
Треугольник COK
подобен треугольнику EOD
, поэтому \frac{CO}{OE}=\frac{CK}{DE}=\frac{7}{2}
.
Пусть площадь трапеции равна S
. Тогда
S=\frac{AD+BC}{2}\cdot h=\frac{7}{2}h,~S_{\triangle CED}=\frac{1}{2}DE\cdot h=h,
значит, S_{\triangle CED}=\frac{2}{7}S
, а так как \frac{CO}{OD}=\frac{7}{2}
, то CO=\frac{7}{9}CE
. Следовательно (см. задачу 3000),
S_{AMOE}=S_{\triangle COD}=\frac{7}{9}S_{\triangle CED}=\frac{7}{9}\cdot\frac{2}{7}S=\frac{2}{9}S.
Источник: ЕГЭ. — 2016

