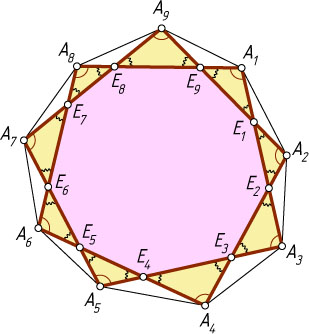
6997. На плоскости изображён выпуклый девятиугольник A_{1}A_{2}\dots A_{9}
. Найдите сумму углов «звёздочки» A_{1}A_{3}A_{5}A_{7}A_{9}A_{2}A_{4}A_{6}A_{8}
.
Ответ. 900^{\circ}
.
Решение. Пусть E_{1}
— точка пересечения отрезков A_{1}A_{3}
и A_{9}A_{2}
, E_{2}
— точка пересечения отрезков A_{2}A_{4}
и A_{1}A_{3}
и т. д., E_{9}
— точка пересечения отрезков A_{8}A_{1}
и A_{9}A_{2}
.
Сумма внешних углов выпуклого девятиугольника E_{1}E_{2}\dots E_{9}
, взятых по одному при каждой вершине, равна 360^{\circ}
(см. задачу 1304), т. е.
\angle A_{1}E_{9}E_{1}+\angle A_{2}E_{1}E_{2}+\dots+\angle A_{8}E_{8}E_{9}=
=\angle A_{1}E_{1}E_{9}+\angle A_{2}E_{2}E_{1}+\dots+\angle A_{9}E_{9}E_{8}=360^{\circ}.
Сумма всех углов треугольников A_{1}E_{9}E_{1}
, A_{2}E_{1}E_{2}
, …, A_{9}E_{8}E_{9}
равна
\angle A_{1}+\angle A_{2}+\dots+\angle A_{9}+360^{\circ}+360^{\circ}=9\cdot180^{\circ}.
Следовательно, сумма углов «звёздочки» равна
9\cdot180^{\circ}-2\cdot360^{\circ}=5\cdot180^{\circ}=900^{\circ}.
Источник: Соросовская олимпиада. — 1994, I, 1-й (заочный) тур, 9 класс
