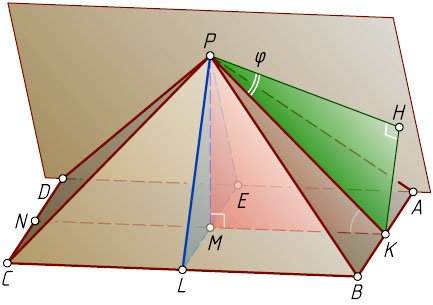
7019. Боковая грань правильной четырёхугольной пирамиды образует с плоскостью основания угол 45^{\circ}
. Найдите угол между апофемой пирамиды и плоскостью соседней грани.
Ответ. 30^{\circ}
.
Решение. Пусть ABCDP
— данная правильная четырёхугольная пирамида с вершиной P
; AB=BC=CD=AD=a
; M
— центр квадрата ABCD
; K
, L
, N
и E
— середины отрезков AB
, BC
, CD
и AD
соответственно.
Поскольку PK\perp AB
и MK\perp AB
, угол PKM
— линейный угол двугранного угла между плоскостью боковой грани ABP
и плоскостью основания пирамиды. По условию \angle PKM=45^{\circ}
.
Апофему PK
пирамиды находим из прямоугольного треугольника PKM
:
PK=\frac{KM}{\cos\angle PKM}=\frac{\frac{a}{2}}{\cos45^{\circ}}=\frac{a\sqrt{2}}{2}.
Найдём угол между апофемой PK
и плоскостью грани APD
. Пусть H
— ортогональная проекция точки K
на плоскость грани APD
, \varphi
— искомый угол. Тогда \varphi=\angle KPH
и \sin\varphi=\frac{KH}{PK}
.
Поскольку K
— середина отрезка AB
, расстояние KH
от точки K
до плоскости грани APD
вдвое меньше расстояния от точки B
до этой плоскости (см. задачу 9180), а так как прямая BC
параллельна плоскости APD
, то все её точки равноудалены от этой плоскости. Поскольку EPL
— равнобедренный прямоугольный треугольник с гипотенузой EL=a
, расстояние от точки L
до плоскости грани APD
равно \frac{a\sqrt{2}}{2}
. Поэтому
KH=\frac{1}{2}LP=\frac{a\sqrt{2}}{4}.
Значит,
\sin\varphi=\frac{KH}{PK}=\frac{\frac{a\sqrt{2}}{4}}{\frac{a\sqrt{2}}{2}}=\frac{1}{2}.
Следовательно, \varphi=30^{\circ}
.