7242. Дан правильный тетраэдр с ребром a
. Найдите объём многогранника, полученного в пересечении этого тетраэдра со своим образом при симметрии относительно середины высоты.
Ответ. \frac{a^{3}\sqrt{2}}{54}
.
Указание. Пересечение данных тетраэдров есть параллелепипед.
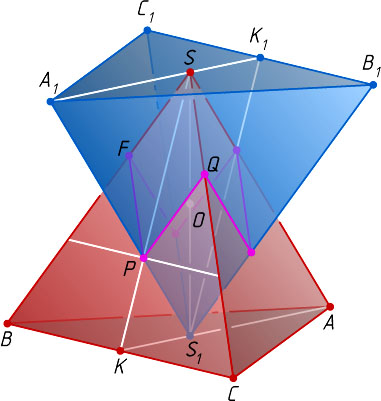
Решение. Пусть SABC
— данный правильный тетраэдр; O
— середина его высоты SS_{1}
; A_{1}
, B_{1}
, C_{1}
— точки, симметричные точкам соответственно A
, B
, C
относительно точки O
. Тогда S_{1}A_{1}B_{1}C_{1}
— образ тетраэдра SABC
при симметрии относительно точки O
.
Образ K_{1}
середины K
ребра BC
при рассматриваемой симметрии — середина ребра B_{1}C_{1}
. Поскольку A_{1}K_{1}\parallel AK
, прямые A_{1}K_{1}
и AK
лежат в одной плоскости. Поэтому прямые A_{1}S_{1}
и KS
пересекаются, причём точка P
их пересечения является точкой пересечения ребра A_{1}S_{1}
тетраэдра S_{1}A_{1}B_{1}C_{1}
с плоскостью грани SBC
тетраэдра SABC
.
Из подобия треугольников KS_{1}P
и SA_{1}P
находим, что
\frac{KP}{PS}=\frac{KS_{1}}{SA_{1}}=\frac{KS_{1}}{2SK_{1}}=\frac{KS_{1}}{2S_{1}K}=\frac{1}{2},~\frac{S_{1}P}{PA_{1}}=\frac{1}{2},
т. е. точка P
делит апофему SK
тетраэдра SABC
и ребро A_{1}S_{1}
тетраэдра S_{1}A_{1}B_{1}C_{1}
в отношении \frac{1}{2}
.
Аналогично находим остальные пять точек пересечения боковых рёбер каждого из этих тетраэдров с плоскостями боковых граней другого. Таким образом, мы построили шесть вершин многогранника пересечения. Ещё две его вершины — точки S
и S_{1}
.
Пусть Q
и F
— вершины искомого многогранника, лежащие на рёбрах SC
и SB
соответственно. Тогда \frac{SQ}{SC}=\frac{SF}{SB}=\frac{1}{3}
. Поэтому SQ=SF=\frac{a}{3}
. Если через точку P
провести прямую, параллельную BC
, то в отсечённом этой прямой от SBC
треугольнике PQ
и PF
будут средними линиями. Поэтому QP\parallel SF
и FP\parallel SQ
. Следовательно, четырёхугольник SQPF
— параллелограмм, а так как SF=SQ
, то это ромб со стороной \frac{a}{3}
. Острый угол ромба равен 60^{\circ}
.
Аналогично докажем, что остальные пять граней искомого многогранника — ромбы со стороной \frac{a}{3}
и острым углом 60^{\circ}
. Следовательно, это параллелепипед.
Объём такого параллелепипеда равен (см. задачу 7214)
\frac{\left(\frac{a}{3}\right)^{3}\sqrt{2}}{2}=\frac{a^{3}\sqrt{2}}{54}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1974, вариант 1, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 205
