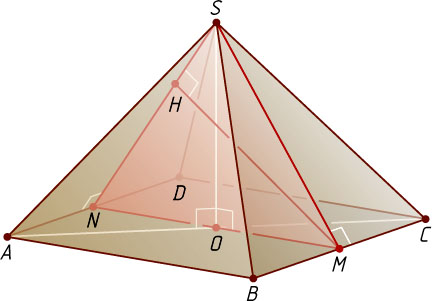
7349. В правильной четырёхугольной пирамиде SABCD
, все рёбра которой равны 1, найдите расстояние между прямыми SA
и BC
.
Ответ. \frac{\sqrt{6}}{3}
.
Решение. Первый способ. Прямая BC
параллельна плоскости SAD
, содержащей прямую SA
, так как BC\parallel AD
. Значит, расстояние между прямыми SA
и BC
равно расстоянию от любой точки прямой BC
(в частности, от середины M
ребра BC
) до плоскости SAD
(см. задачу 7889).
Опустим перпендикуляр MH
из точки M
на апофему SN
, лежащую в грани SAD
. По признаку перпендикулярности прямой и плоскости прямая AD
перпендикулярна плоскости SMN
, содержащей прямую MH
, так как AD\perp MN
и AD\perp SN
. Значит, прямая AD
перпендикулярна любой прямой плоскости SMN
, в частности, прямой MH
. Таким образом, прямая MH
перпендикулярна двум пересекающимся прямым SN
и AD
плоскости SAD
. Следовательно, MH
(высота треугольника SMN
) — перпендикуляр к плоскости SAD
.
Отрезок SN
— высота равностороннего треугольника ASD
, поэтому SN=\frac{AD\sqrt{3}}{2}=\frac{\sqrt{3}}{2}
. Пусть O
— центр квадрата ABCD
. Из прямоугольного треугольника AOS
находим, что
SO=\sqrt{SA^{2}-OA^{2}}=\sqrt{1-\frac{1}{2}}=\frac{\sqrt{2}}{2}.
Записав двумя способами площадь равнобедренного треугольника SMN
, получим, что \frac{1}{2}MN\cdot SO=\frac{1}{2}SN\cdot MH
, откуда
MH=\frac{MN\cdot SO}{SN}=\frac{1\cdot\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}=\sqrt{\frac{2}{3}}=\frac{\sqrt{6}}{3}.
Второй способ. Воспользуемся следующей формулой объёма тетраэдра: V=\frac{1}{6}abd\sin\alpha
, где a
и b
— длины противоположных рёбер тетраэдра, d
— расстояние между прямыми, содержащими эти рёбра, \alpha
— угол между этими прямыми.
Рассмотрим тетраэдр ABCS
. Его объём равен половине объёма данной пирамиды SABCD
, т. е.
V_{ABCS}=\frac{1}{2}\cdot\frac{1}{3}\cdot1\cdot\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{12}.
С другой стороны
V_{ABCS}=\frac{1}{6}BC\cdot AC\cdot d\sin60^{\circ}=\frac{1}{6}\cdot1\cdot1\cdot d\cdot\frac{\sqrt{3}}{2}=\frac{d\sqrt{3}}{12}
(\alpha=\angle SAD=60^{\circ}
). Из равенства \frac{\sqrt{2}}{12}=\frac{d\sqrt{3}}{12}
находим, что d=\sqrt{\frac{2}{3}}=\frac{\sqrt{6}}{3}
.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 6.1, с. 10
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3(б), с. 55
