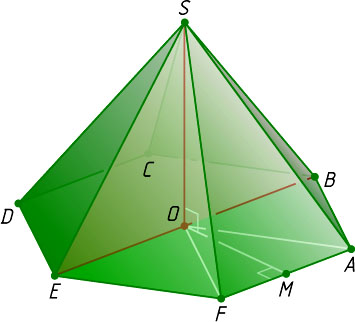
7357. В правильной шестиугольной пирамиде SABCDEF
с основанием ABCDEF
найдите расстояние между прямыми SB
и AF
, если известно, что стороны основания равны 1.
Ответ. \frac{\sqrt{3}}{2}
.
Решение. Плоскость SBE
проходит через прямую SB
и прямую BE
, параллельную AF
, значит, расстояние между прямыми SB
и AF
равно расстоянию от любой точки прямой AF
до плоскости SBE
(см. задачу 7889).
Пусть O
— центр правильного шестиугольника ABCDEF
, а M
— середина AF
. Отрезок MO
— высота равностороннего треугольника AOF
, поэтому MO\perp AF
, а так как BE\parallel AF
, то MO\perp BE
. Кроме того, прямая MO
лежит в плоскости ABCDEF
, перпендикулярной прямой SO
, поэтому MO\perp SO
. Таким образом, прямая MO
перпендикулярна двум пересекающимся прямым BE
и SO
плоскости SBE
, значит, MO
— перпендикуляр к этой плоскости. Следовательно, расстояние между прямыми SB
и AF
равно длине отрезка MO
, а так как MO
— высота равностороннего треугольника AOF
, то MO=\frac{AF\sqrt{3}}{2}=\frac{\sqrt{3}}{2}
.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 6, с. 41
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6(а), с. 55
