7369. В правильной шестиугольной призме ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}
, все рёбра которой равны 1, найдите расстояние между прямыми BB_{1}
и FE_{1}
.
Ответ. \sqrt{3}
.
Решение. Прямая BB_{1}
параллельна плоскости EE_{1}F_{1}F
, содержащей прямую FE_{1}
, так как BB_{1}\parallel FF_{1}
. Значит, расстояние между прямыми BB_{1}
и FE_{1}
равно расстоянию от любой точки прямой BB_{1}
(в частности, от точки B
) до плоскости EE_{1}F_{1}F
(см. задачу 7889).
Заметим, что диагональ BF
правильного шестиугольника ABCDEF
перпендикулярна стороне EF
. Кроме того, прямая FF_{1}
перпендикулярна плоскости ABCDEF
, поэтому BF\perp FF_{1}
. Таким образом, прямая BF
перпендикулярна двум пересекающимся прямым EF
и FF_{1}
плоскости EE_{1}F_{1}F
, значит, по признаку перпендикулярности прямой и плоскости прямая BF
перпендикулярна плоскости EE_{1}F_{1}F
. Следовательно, расстояние между прямыми BB_{1}
и FE_{1}
равно длине отрезка BF
. Из равнобедренного треугольника BAF
по теореме косинусов находим, что
BF=\sqrt{AB^{2}+AF^{2}-2AB\cdot AF\cos120^{\circ}}=\sqrt{1+1-2\cdot\left(-\frac{1}{2}\right)}=\sqrt{3}.
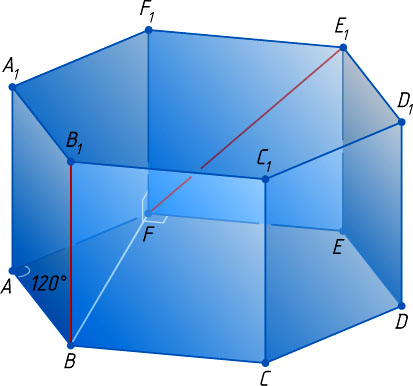
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 17, с. 54
