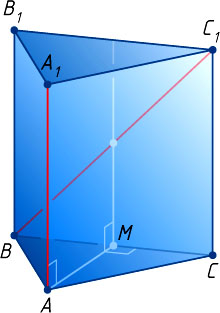
7462. В правильной треугольной призме ABCA_{1}B_{1}C_{1}
, все рёбра которой равны 1, найдите расстояние между прямыми AA_{1}
и BC_{1}
.
Ответ. \frac{\sqrt{3}}{2}
.
Решение. Прямая AA_{1}
параллельна плоскости BB_{1}C_{1}C
, так как эта прямая параллельна прямой BB_{1}
, лежащей в плоскости BB_{1}C_{1}C
. Значит, расстояние между прямыми AA_{1}
и BC_{1}
равно расстоянию от любой точки прямой AA_{1}
, например, от точки A
, до плоскости BB_{1}C_{1}C
(см. задачу 7889).
Пусть M
— середина ребра BC
. Тогда AM\perp BC
как медиана, а значит, и высота равностороннего треугольника ABC
, а также AM\perp AA_{1}
, так как прямая AA_{1}
перпендикулярна плоскости ABC
, содержащей прямую AM
. Поэтому AM
— перпендикуляр к плоскости BB_{1}C_{1}C
. Следовательно, расстояние между прямыми AA_{1}
и BC_{1}
равно длине отрезка AM
, т. е. \frac{\sqrt{3}}{2}
.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 16, с. 54
