8208. В пирамиде ABCD
двугранный угол при ребре AC
равен 90^{\circ}
, AB=BC=CD
, BD=AC
. Найдите двугранный угол при ребре AD
.
Ответ. 60^{\circ}
.
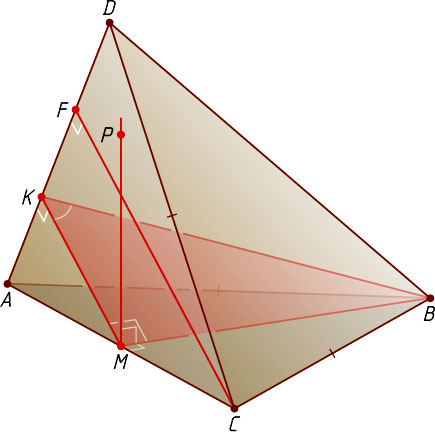
Решение. Первый способ. Опустим перпендикуляр BM
из вершины B
данной пирамиды на ребро AC
, а из точки M
в плоскости ACD
проведём перпендикуляр MP
к AC
. Тогда BMP
— линейный угол двугранного угла с ребром AC
. По условию задачи \angle BMP=90^{\circ}
. Поэтому прямая BM
перпендикулярна двум пересекающимся прямым AC
и MP
плоскости ADC
. Значит, прямая BM
перпендикулярна плоскости ADC
.
Точка M
— середина AC
, так как высота BM
равнобедренного треугольника ABC
является его медианой (AB=BC
по условию). Пусть BK
— высота треугольника ABD
. Тогда по теореме о трёх перпендикулярах MK\perp AD
. Значит, BKM
— линейный угол двугранного угла с ребром AD
.
Пусть CF
— высота треугольника ACD
. Тогда MK=\frac{1}{2}CF
как средняя линия треугольника ACF
. Из равенства треугольников ABD
и DCA
следует равенство соответствующих высот этих треугольников. Поэтому BK=CF
, а MK=\frac{1}{2}CF=\frac{1}{2}BK
. Таким образом, в прямоугольном треугольнике BMK
катет MK
равен половине гипотенузы BK
. Следовательно, \angle BKM=60^{\circ}
.
Второй способ. Поскольку плоскости ABC
и ACD
— перпендикулярны (двугранный угол между ними равен 90^{\circ}
), высота BM
треугольника ABC
является перпендикуляром к плоскости ACD
, значит, треугольник AMD
— ортогональная проекция треугольника ABD
на плоскость ACD
, а так как треугольник ABC
равнобедренный (AB=BC)
, то M
— середина AC
.
Треугольники ACD
и DBA
равны по трём сторонам, а DM
— медиана треугольника ADC
, поэтому
S_{\triangle AMD}=\frac{1}{2}S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABD}.
Обозначим через \alpha
искомый угол между гранями BAD
и CAD
. Тогда (см. задачу 8093)
\cos\alpha=\frac{S_{\triangle AMD}}{S_{\triangle ABD}}=\frac{\frac{1}{2}S_{\triangle ABD}}{S_{\triangle ABD}}=\frac{1}{2}.
Следовательно, \alpha=60^{\circ}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 17, с. 40
