8222. Ребро BD
пирамиды ABCD
перпендикулярно плоскости ADC
. Докажите, что сечением этой пирамиды плоскостью, проходящей через точку D
и середины рёбер AB
и BC
, является треугольник, подобный треугольнику ABC
. Чему равен коэффициент подобия?
Ответ. \frac{1}{2}
.
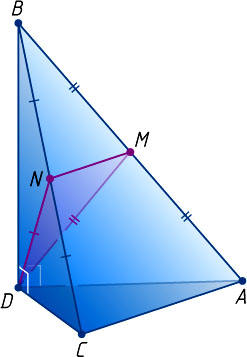
Решение. Пусть M
и N
— середины рёбер AB
и BC
соответственно. Тогда MN
— средняя линия треугольника ABC
. Поэтому MN=\frac{1}{2}AC
. Прямая BD
перпендикулярна плоскости ACD
, поэтому треугольники ABD
и CBD
— прямоугольные. Их медианы DM
и DN
, проведённые из вершин прямых углов, равны половинам гипотенуз (см. задачу 1109), т. е. DM=\frac{1}{2}AB
и DN=\frac{1}{2}BC
. Следовательно, треугольник MDN
подобен треугольнику ABC
с коэффициентом \frac{1}{2}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 3, с. 52
