8384. В треугольной пирамиде ABCD
известно, что AB=a
и \angle ACB=\angle ADB=90^{\circ}
. Найдите радиус сферы, описанной около этой пирамиды.
Ответ. \frac{a}{2}
.
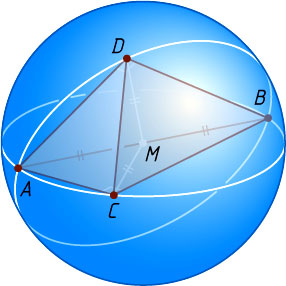
Решение. Пусть M
— середина AB
. Так как в прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы (см. задачу 1109), то MC=MA=MB=MD=\frac{a}{2}
. Значит, точка M
удалена от каждой вершины данной пирамиды на одно и то же расстояние, равное \frac{a}{2}
. Следовательно, M
— центр сферы, описанной около данной пирамиды, а радиус сферы равен \frac{a}{2}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 13, с. 89
