8440. Из вершин основания тетраэдра в боковых гранях проводят высоты, и в каждой из боковых граней через основания двух лежащих в ней высот проводят прямую. Докажите, что эти три прямые параллельны одной плоскости. (Можно считать, что плоские углы при вершине тетраэдра отличны от 90^{\circ}
.)
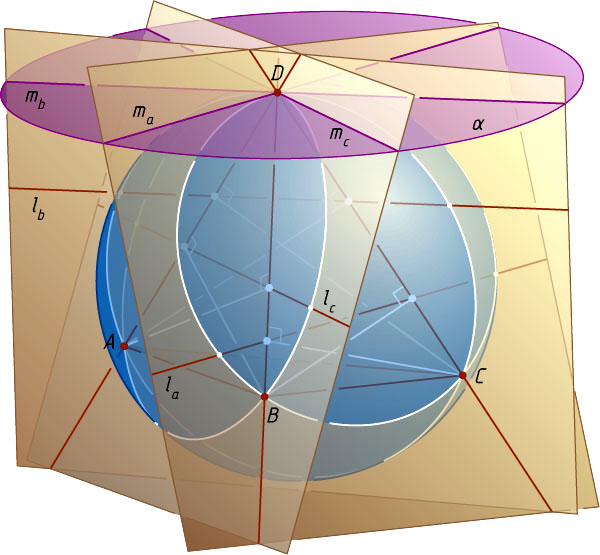
Решение. Первый способ. Рассмотрим тетраэдр ABCD
. Пусть l_{a}
— прямая, проходящая через основания высот грани BCD
, проведённых из вершин B
и C
. Аналогично определяется прямая l_{b}
в плоскости ACD
и прямая l_{c}
в плоскости ABD
. Нужно доказать, что прямые l_{a}
, l_{b}
и l_{c}
параллельны одной плоскости.
Лемма. Пусть BM
и CN
— высоты треугольника BCD
, а m
— касательная к описанной окружности треугольника, проведённая через точку D
. Тогда MN\parallel m
.
Доказательство. Пусть K
— точка на прямой m
, причём точки K
и C
расположены по разные стороны от прямой BD
. Из теоремы об угле между касательной и хордой следует, что \angle BDK=\angle BCD
, а так как \angle BCD=\angle MND
, то \angle BDK=\angle MND
. Следовательно, DK\parallel MN
. Лемма доказана.
Перейдём к нашей задаче. Опишем сферу около тетраэдра ABCD
и проведём к ней касательную плоскость \alpha
через вершину D
. В сечении сферы плоскостью BCD
получим окружность, описанную около треугольника BCD
, и касательную m_{a}
к этой окружности, проходящую через точку D
.
Пусть BM
и CN
— высоты треугольника BCD
. По доказанной лемме прямая MN
(т. е. прямая l_{a}
) параллельна m_{a}
. Следовательно, прямая l_{a}
параллельна плоскости \alpha
. Аналогично для прямых l_{b}
и l_{c}
.
Второй способ. Пусть DA=a
, DB=b
, DC=c
. На лучах DA
, DB
, DC
отложим отрезки DA_{1}
, DB_{1}
, DC_{1}
, равные по длине произведениям bc
, ac
, ab
соответственно. Докажем, что прямые, о которых говорится в условии задачи, параллельны прямым A_{1}B_{1}
, B_{1}C_{1}
, A_{1}C_{1}
, а значит, параллельны плоскости A_{1}B_{1}C_{1}
.
Пусть BM
и CN
— высоты треугольника BDC
. Треугольники DMN
и DB_{1}C_{1}
подобны (см. задачу 19), поэтому
\frac{DM}{DN}=\frac{DB}{DC}=\frac{b}{c}=\frac{ab}{ac}=\frac{DC_{1}}{DB_{1}}.
Следовательно, MN\parallel B_{1}C_{1}
. Аналогично для двух остальных отрезков.
Третий способ. Пусть BM
и CN
— высоты треугольника BDC
. Обозначим \overrightarrow{DA}=\overrightarrow{a}
, \overrightarrow{DB}=\overrightarrow{b}
, \overrightarrow{DC}=\overrightarrow{c}
. \angle BDC=\alpha
. Тогда
\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{DN}=\overrightarrow{DN}-\overrightarrow{DM}=c\cos\alpha\cdot\frac{1}{b}\overrightarrow{b}-b\cos\alpha\cdot\frac{1}{c}\overrightarrow{c}=
=\left(\frac{1}{b^{2}}\overrightarrow{b}-\frac{1}{c^{2}}\overrightarrow{c}\right)bc\cos\alpha=\left(\frac{1}{b^{2}}\overrightarrow{b}-\frac{1}{c^{2}}\overrightarrow{c}\right)\cdot(\overrightarrow{b},\overrightarrow{c}),
где (\overrightarrow{b},\overrightarrow{c})
— скалярное произведение векторов \overrightarrow{b}
и \overrightarrow{c}
.
Аналогичная формула верна и для двух других граней тетраэдра. Но сумма трёх векторов
\frac{1}{b^{2}}\overrightarrow{b}-\frac{1}{c^{2}}\overrightarrow{c},~\frac{1}{a^{2}}\overrightarrow{a}-\frac{1}{b^{2}}\overrightarrow{b}~\mbox{и}~\frac{1}{c^{2}}\overrightarrow{c}-\frac{1}{b^{2}}\overrightarrow{a}
равна нулевому вектору, значит, эти векторы компланарны. Следовательно, параллельные им прямые, о которых говорится в условии задачи, параллельны одной плоскости.

Примечание. Утверждение верно для любой пирамиды, около которой можно описать сферу.
Автор: Шарыгин И. Ф.
Источник: Турнир городов. — 1983-1984, V, весенний тур, старшие классы, основной вариант
Источник: Журнал «Квант». — 1984, № 6, с. 33, М868; 1984, № 9, с. 39-40, М868
Источник: Задачник «Кванта». — М868
Источник: Прасолов В. В. Задачи по стереометрии. — 2-е изд. — М.: МЦНМО, 2016. — № 9.6, с. 143

