8595. Площади граней ABC
и ADC
тетраэдра ABCD
равны P
и Q
, двугранный угол между ними равен \alpha
. Найдите площадь треугольника, по которому биссекторная плоскость указанного угла пересекает тетраэдр.
Ответ. \frac{2P\cdot Q\cos\frac{\alpha}{2}}{P+Q}
.
Указание. См. задачу 8301.
Решение. Докажем сначала следующее утверждение: если V
— объём тетраэдра, S_{1}
и S_{2}
— площади двух граней, a
— длина их общего ребра, \varphi
— величина двугранного угла между ними, то V=\frac{2}{3}\cdot\frac{S_{1}S_{2}\cdot\sin\varphi}{a}
.
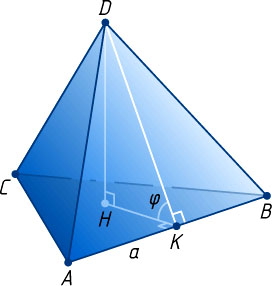
Пусть ребро AB
тетраэдра ABCD
равно a
(рис. 1), угол между гранями ABC
и ABD
равен \varphi
, S_{\triangle ABC}=S_{1}
, S_{\triangle ABD}=S_{2}
.
Если DH
— высота тетраэдра, опущенная на основание ABC
, а HK
— перпендикуляр, опущенный из точки H
на AB
, то по теореме о трёх перпендикулярах DK\perp AB
, значит, DKH
— линейный угол двугранного угла тетраэдра при ребре AB
. Поэтому \angle DKH=\varphi
. Тогда
V=V_{ABCD}=\frac{1}{3}S_{\triangle ABC}\cdot DH=\frac{1}{3}S_{1}\cdot DK\sin\varphi=\frac{1}{3}S_{1}\cdot\frac{2S_{2}}{a}\cdot\sin\varphi=\frac{2}{3}\cdot\frac{S_{1}S_{2}\cdot\sin\varphi}{a}.
Утверждение доказано.
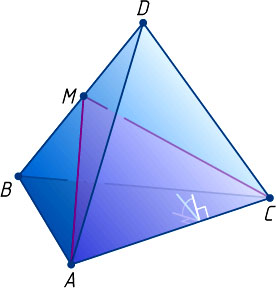
Перейдём к нашей задаче (рис. 2). Пусть M
— точка пересечения указанной биссекторной плоскости с ребром BD
, S
— площадь треугольника AMC
. Применяя доказанную формулу к тетраэдрам ABCD
, MABC
и MACD
, получим, что
V_{ABCD}=\frac{2}{3}\cdot\frac{P\cdot Q\cdot\sin\alpha}{AC},~V_{MABC}=\frac{2}{3}\cdot\frac{P\cdot S\cdot\sin\frac{\alpha}{2}}{AC},~V_{MACD}=\frac{2}{3}\cdot\frac{Q\cdot S\cdot\sin\frac{\alpha}{2}}{AC},
а так как V_{ABCD}=V_{MABC}+V_{MACD}
, то
\frac{2}{3}\cdot\frac{P\cdot Q\cdot\sin\alpha}{AC}=\frac{2}{3}\cdot\frac{P\cdot S\cdot\sin\frac{\alpha}{2}}{AC}+\frac{2}{3}\cdot\frac{Q\cdot S\cdot\sin\frac{\alpha}{2}}{AC}.
Из этого уравнения находим, что
S=\frac{P\cdot Q\sin\alpha}{\sin\frac{\alpha}{2}(P+Q)}=\frac{2P\cdot Q\cos\frac{\alpha}{2}}{P+Q}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 2, с. 133

