8727. Сторона основания ABC
правильной треугольной пирамиды ABCD
равна 6, двугранный угол между боковыми гранями равен \arccos\frac{7}{32}
. Точки A_{1}
и B_{1}
— середины рёбер AD
и BD
соответственно, BC_{1}
— высота в треугольнике DBC
. Найдите:
1) угол между прямыми AB
и B_{1}C_{1}
;
2) площадь треугольника A_{1}B_{1}C_{1}
;
3) расстояние от точки B
до плоскости A_{1}B_{1}C_{1}
;
4) радиус вписанного в пирамиду A_{1}B_{1}C_{1}D
шара.
Ответ. \arccos\frac{3}{5}
; 3; \frac{21\sqrt{39}}{100}
; \frac{7\sqrt{39}}{104}
.
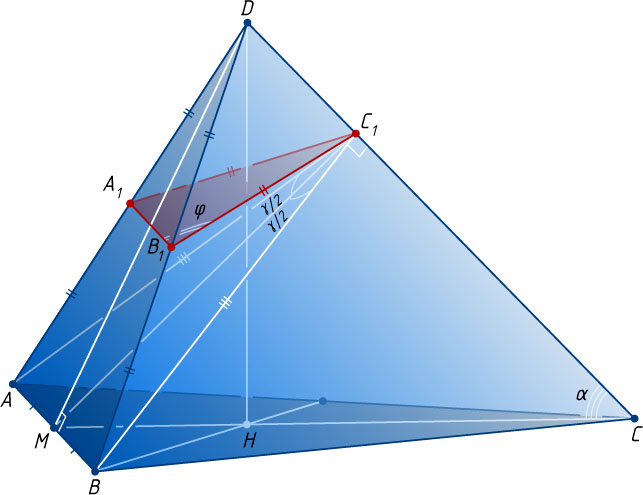
Решение. Пусть DH
— высота пирамиды, M
— середина AB
. Прямая CD
перпендикулярна двум пересекающимся прямым AB
и BC_{1}
плоскости AC_{1}B
, поэтому AC_{1}B
— линейный угол двугранного угла между гранями ADC
и BDC
. Обозначим \angle AC_{1}B=\gamma
. По условию задачи \cos\gamma=\frac{7}{32}
. Кроме того, BC_{1}\perp CD
и AC_{1}\perp CD
, значит, прямоугольные треугольники DC_{1}B
и DC_{1}A
равны по катету и гипотенузе, поэтому AC_{1}B
— равнобедренный треугольник.
Подставив значение \cos\gamma
в формулу \cos\gamma=\frac{1-\tg^{2}\frac{\gamma}{2}}{1+\tg^{2}\frac{\gamma}{2}}
, получим уравнение \frac{7}{32}=\frac{1-\tg^{2}\frac{\gamma}{2}}{1+\tg^{2}\frac{\gamma}{2}}
, из которого находим, что \tg\frac{\gamma}{2}=\frac{5}{\sqrt{39}}
. Из равнобедренного треугольника AC_{1}B
находим, что
MC_{1}=\frac{BM}{\tg\frac{\gamma}{2}}=\frac{3\sqrt{39}}{5}.
Обозначим \angle DCH=\alpha
. Тогда
\sin\alpha=\frac{MC_{1}}{MC}=\frac{MC_{1}}{\frac{AB\sqrt{3}}{2}}=\frac{\frac{3\sqrt{39}}{5}}{\frac{6\sqrt{3}}{2}}=\frac{\sqrt{13}}{5},
\cos\alpha=\sqrt{1-\sin^{2}\alpha}=\sqrt{1-\frac{13}{25}}=\frac{2\sqrt{3}}{5},~\tg\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{\sqrt{13}}{2\sqrt{3}}.
Из прямоугольных треугольников CDH
и BDC_{1}
находим, что
DH=CH\tg\alpha=2\sqrt{3}\cdot\frac{\sqrt{13}}{2\sqrt{3}}=\sqrt{13},~DC=\frac{HC}{\cos\alpha}=\frac{\frac{AB\sqrt{3}}{3}}{\cos\alpha}=\frac{\sqrt{3}}{\frac{2\sqrt{3}}{5}}=5,
BC_{1}=\sqrt{MC_{1}^{2}+BM^{2}}=\sqrt{\left(\frac{3\sqrt{39}}{5}\right)^{2}+9}=\frac{24}{5}.
Тогда
DC_{1}=\sqrt{BD^{2}-BC_{1}^{2}}=\sqrt{25-\left(\frac{24}{5}\right)^{2}}=\frac{7}{5}.
Поскольку B_{1}C_{1}
— медиана прямоугольного треугольника BC_{1}D
,
B_{1}C_{1}=\frac{1}{2}DB=\frac{1}{2}DC=\frac{5}{2}
(см. задачу 1109). Треугольник A_{1}DC_{1}
равен равнобедренному треугольнику B_{1}DC_{1}
по двум сторонам и углу между ними, поэтому A_{1}C_{1}=B_{1}C_{1}=\frac{5}{2}
. Обозначим \angle A_{1}B_{1}C_{1}=\varphi
. Поскольку A_{1}B_{1}\parallel AB
, угол между прямыми AB
и B_{1}C_{1}
равен углу между прямыми A_{1}B_{1}
и B_{1}C_{1}
. Из равнобедренного треугольника A_{1}B_{1}C_{1}
находим, что
\cos\varphi=\frac{\frac{A_{1}B_{1}}{2}}{B_{1}C_{1}}=\frac{\frac{3}{2}}{\frac{5}{2}}=\frac{3}{5}.
Тогда \sin\varphi=\frac{4}{5}
и
S_{\triangle A_{1}B_{1}C_{1}}=\frac{1}{2}A_{1}B_{1}\cdot B_{1}C_{1}\sin\varphi=\frac{1}{2}\cdot3\cdot\frac{5}{2}\cdot\frac{4}{5}=3.
Пусть h
— расстояние от точки B
до плоскости A_{1}B_{1}C_{1}
. Поскольку B_{1}
— середина отрезка BD
, расстояние от точки D
до плоскости A_{1}B_{1}C_{1}
также равно h
. Пусть V
и V_{1}
— объёмы пирамид ABCD
и A_{1}B_{1}C_{1}D
соответственно. Тогда
V=\frac{1}{3}S_{\triangle ABC}\cdot DH=\frac{1}{3}\cdot\frac{AB^{2}\sqrt{3}}{4}\cdot\sqrt{13}=\frac{1}{3}\cdot\frac{36\sqrt{3}}{4}\cdot\sqrt{13}=3\sqrt{39},
V_{1}=\frac{DA_{1}}{DA}\cdot\frac{DB_{1}}{DB}\cdot\frac{DC_{1}}{DC}\cdot V=\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{\frac{7}{5}}{5}\cdot3\sqrt{39}=\frac{21\sqrt{39}}{100},
а так как высота пирамиды A_{1}B_{1}C_{1}D
равна h
, то
h=\frac{3V_{1}}{S_{\triangle A_{1}B_{1}C_{1}}}=\frac{\frac{3\cdot21\sqrt{39}}{100}}{3}=\frac{21\sqrt{39}}{100}.
Поскольку BC_{1}
— высота треугольника BDC
,
S_{\triangle BDC}=\frac{1}{2}DC\cdot BC_{1}=\frac{1}{2}\cdot5\cdot\frac{24}{5}=12.
Тогда
S_{\triangle B_{1}DC_{1}}=\frac{DB_{1}}{DB}\cdot\frac{DC_{1}}{DC}\cdot S_{\triangle BDC}=\frac{1}{2}\cdot\frac{7}{25}\cdot12=\frac{42}{25}.
Пусть S
— площадь полной поверхности пирамиды A_{1}B_{1}C_{1}D
, r
— радиус шара, вписанного в эту пирамиду.
S=2S_{\triangle A_{1}B_{1}C_{1}}+2S_{\triangle B_{1}DC_{1}}=2\left(3+\frac{42}{25}\right).
Следовательно,
r=\frac{3V_{1}}{S}=\frac{3\cdot\frac{21\sqrt{39}}{100}}{2\left(3+\frac{42}{25}\right)}=\frac{3\cdot21\sqrt{39}}{2\cdot3\left(\frac{14}{25}+1\right)\cdot100}=\frac{3\cdot7\sqrt{39}}{2(56+100)}=\frac{7\sqrt{39}}{104}.
Источник: Вступительный экзамен в МФТИ. — 2005, билет 9, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 05-9-4, с. 443
