8743. Высота конуса с вершиной O
равна 4, образующая конуса равна 5. Пирамида ABCD
вписана в конус так, что точки A
и C
принадлежат окружности основания, точки B
и D
принадлежат боковой поверхности, причём точка B
принадлежит образующей OA
. Треугольники OAC
и OBD
— равносторонние, причём OB=3
. Найдите объём пирамиды, двугранный угол при ребре AB
и радиус сферы, описанной около пирамиды ABCD
.
Ответ. V=\frac{10\sqrt{11}}{9}
; \varphi=2\arcsin\sqrt{\frac{11}{27}}
; R=\sqrt{10}
.
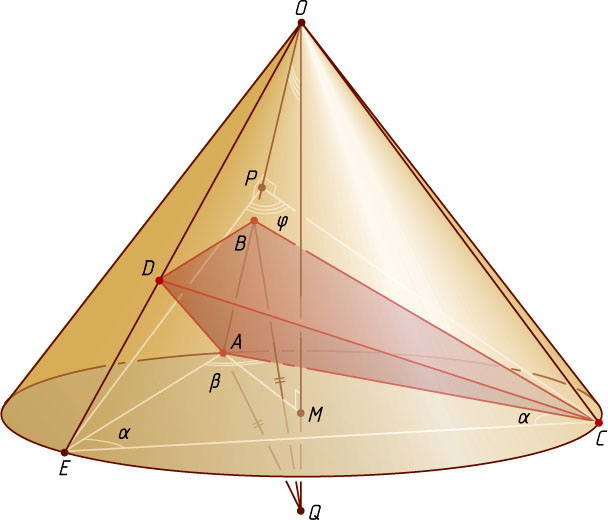
Решение. Пусть OM
— высота конуса, точка D
лежит на образующей OE
конуса (рис. 1), а r
— радиус окружности основания. Тогда
AC=OA=5,~\angle AOE=\angle BOD=60^{\circ},~AE=OA=OE=5,
r=ME=\sqrt{OE^{2}-OM^{2}}=\sqrt{25-16}=3.
Обозначим \angle AEC=\alpha
, \angle CAE=\beta
. Тогда
\sin\alpha=\frac{AC}{2r}=\frac{5}{6},~\cos\alpha=\sqrt{1-\frac{25}{36}}=\frac{\sqrt{11}}{6},
\sin\beta=\sin(180^{\circ}-2\alpha)=\sin2\alpha=2\sin\alpha\cos\alpha=2\cdot\frac{5}{6}\cdot\frac{\sqrt{11}}{6}=\frac{5\sqrt{11}}{18}.
Поскольку треугольники OBD
и OAE
— равносторонние, BD\parallel AE
, значит, угол между скрещивающимися прямыми AC
и BD
равен углу между пересекающимися прямыми AC
и AE
, т. е. синус этого угла равен \sin\beta=\frac{5\sqrt{11}}{18}
.
Пусть d
— расстояние между прямыми AC
и BD
. Прямая BD
параллельна плоскости основания конуса, содержащей прямую AC
, значит, расстояние d
между прямыми AC
и BD
равно расстоянию от точки B
до плоскости основания конуса (см. задачу 7889), а так как высота конуса равна 4 и OB=3
, то
d=OM\cdot\frac{AB}{OA}=4\cdot\frac{5-3}{5}=\frac{8}{5}.
Пусть V
— объём пирамиды ABCD
. Тогда
V=\frac{1}{6}AC\cdot BD\cdot d\sin\beta=\frac{1}{6}\cdot5\cdot3\cdot\frac{8}{5}\cdot\frac{5\sqrt{11}}{18}=\frac{10\sqrt{11}}{9}.
Высоты равносторонних треугольников AOC
и AOE
, опущенные на общую сторону OA
, проходят через середину P
образующей AO
, значит, CPE
— линейный угол двугранного угла между плоскостями AOC
и AOE
, или линейный угол искомого двугранного угла при ребре AB
пирамиды ABCD
. Пусть \angle CPE=\varphi
, а L
— середина основания CE
равнобедренного треугольника ACE
. Тогда
CL=AE\cos\alpha=5\cdot\frac{\sqrt{11}}{6}=\frac{5\sqrt{11}}{6},~\sin\frac{\varphi}{2}=\frac{CL}{CP}=\frac{\frac{5\sqrt{11}}{6}}{\frac{5\sqrt{3}}{2}}=\sqrt{\frac{11}{27}}.
Заметим, что центр Q
сферы, описанной около пирамиды ABCD
, равноудалён от концов отрезка AC
, значит, точка Q
лежит в плоскости, перпендикулярной прямой AC
и проходящей через середину AC
. Аналогично, точка Q
лежит в плоскости, перпендикулярной прямой BD
и проходящей через середину BD
. Эти две плоскости пересекаются по прямой OM
, поэтому центр сферы лежит на прямой OM
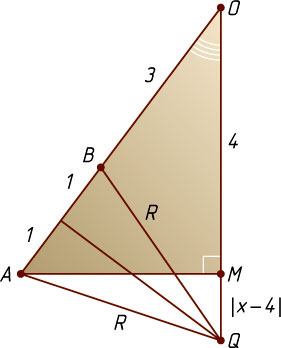
. Обозначим OQ=x
, QB=QA=R
— искомый радиус сферы (рис. 2). Тогда QM=|OQ-OM|=|x-4|
. В треугольниках AMQ
и OBQ
R^{2}=QA^{2}=AM^{2}+MQ^{2}=9+(x-4)^{2},
R^{2}=QB^{2}=OB^{2}+OQ^{2}-2OB\cdot OQ\cos\angle BOQ=9+x^{2}-2\cdot3\cdot x\cdot\frac{4}{5}=9+x^{2}-\frac{24}{5}x.
Из уравнения
9+(x-4)^{2}=9+x^{2}-\frac{24}{5}x
находим, что x=5
. Следовательно,
R^{2}=9+(x-4)^{2}=9+1=10,~R=\sqrt{10}.
