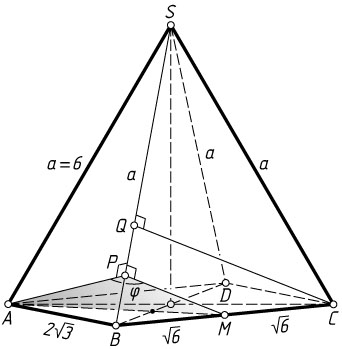
9570. Дана четырёхугольная пирамида SABCD
, в основании которой лежит прямоугольник ABCD
. Основанием высоты пирамиды, является точка пересечения диагоналей основания. Известно, что AB=2\sqrt{3}
, BC=2\sqrt{6}
. Из точек A
и C
опущены перпендикуляры AP
и CQ
на ребро SB
.
а) Докажите, что P
— середина BQ
.
б) Найдите угол между гранями SBA
и SBC
, если AS=6
.
Ответ. 180^{\circ}-\arccos\frac{1}{\sqrt{55}}
.
Решение. а) Высота пирамиды проходит через центр окружности, описанной около основания, значит, боковые рёбра пирамиды равны (см. задачу 7163). Обозначим SA=SB=SC=SD=a
. Тогда
AB^{2}-BP^{2}=AP^{2}=SA^{2}-SP^{2},~\mbox{или}~12-BP^{2}=a^{2}-(a-BP)^{2},
откуда BP=\frac{6}{a}
. Из равнобедренного треугольника BSC
аналогично находим, что BQ=\frac{12}{a}
. Следовательно, BP=\frac{1}{2}BQ
, т. е. P
— середина BQ
.
б) В равнобедренном треугольнике BSC
через точку P
, лежащую на боковой стороне SB
, проведём прямую, параллельную высоте CQ
. Пусть M
— точка её пересечения со стороной BC
. По теореме Фалеса M
— середина BC
. Значит,
PM=\frac{1}{2}CQ=\frac{1}{2}\sqrt{BC^{2}-BQ^{2}}=\frac{1}{2}\sqrt{24-\left(\frac{12}{a}\right)^{2}}=\frac{1}{2}\sqrt{24-4}=\sqrt{5}.
Из равнобедренного треугольника ASB
находим, что
AP=\sqrt{AB^{2}-BP^{2}}=\sqrt{12-\left(\frac{6}{a}\right)^{2}}=\sqrt{12-1}=\sqrt{11}.
Из прямоугольного треугольника ABM
находим, что
AM^{2}=AB^{2}+BM^{2}=12+6=18.
Поскольку AP\perp SB
и MP\perp SB
, угол APM=\varphi
— линейный угол двугранного угла между гранями SBA
и SBC
. По теореме косинусов
\cos\varphi=\frac{AP^{2}+MP^{2}-AM^{2}}{2AP\cdot MP}=\frac{11+5-18}{2\cdot\sqrt{11}\cdot\sqrt{5}}=-\frac{1}{\sqrt{55}}.
Следовательно, \varphi=180^{\circ}-\arccos\frac{1}{\sqrt{55}}
.
Источник: ЕГЭ. — 2017, 2 июня
