9571. Основанием прямой треугольной призмы ABCA_{1}B_{1}C_{1}
является прямоугольный треугольник ABC
с прямым углом C
. Прямые CA_{1}
и AB_{1}
перпендикулярны.
а) Докажите, что AA_{1}=AC
.
б) Найдите расстояние между прямыми CA_{1}
и AB_{1}
, если BC=8
и AC=7
.
Ответ. \frac{28}{9}
.
Решение. а) Прямая BC
перпендикулярна плоскости ACA_{1}
, так как BC\perp AC
и BC\perp AA_{1}
. Поскольку B_{1}C_{1}\parallel BC
, то B_{1}C_{1}
— перпендикуляр к плоскости ACA_{1}
, а AC_{1}
— ортогональная проекция наклонной AB_{1}
на эту плоскость. По условию задачи CA_{1}\perp AB_{1}
, значит, по теореме о трёх перпендикулярах AC_{1}\perp CA_{1}
. Диагонали прямоугольника AA_{1}C_{1}C
перпендикулярны, значит, это квадрат. Следовательно, AA_{1}=AC
.
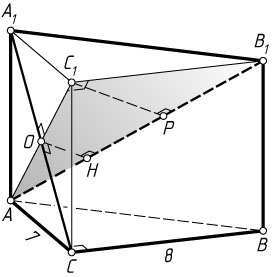
б) Пусть H
— основание перпендикуляра, опущенного из центра O
квадрата AA_{1}C_{1}C
на прямую AB_{1}
. Прямая CA_{1}
перпендикулярна плоскости AC_{1}B_{1}
, так как CA_{1}\perp AC_{1}
и CA_{1}\perp B_{1}C_{1}
. Значит, OH\perp AC_{1}
, и OH
— общий перпендикуляр скрещивающихся прямых CA_{1}
и AB_{1}
. Тогда расстояние между эти прямыми равно длине отрезка OH
, т. е. половине высоты C_{1}P
прямоугольного треугольника AC_{1}B_{1}
, опущенной из вершины прямого угла. Из прямоугольных треугольников ACC_{1}
и AC_{1}B_{1}
находим, что
AC_{1}=7\sqrt{2},~AB_{1}=\sqrt{AC_{1}^{2}+B_{1}C_{1}^{2}}=\sqrt{98+64}=9\sqrt{2},
поэтому
C_{1}P=\frac{AC_{1}\cdot B_{1}C_{1}}{AB_{1}}=\frac{7\sqrt{2}\cdot8}{9\sqrt{2}}=\frac{56}{9}
(см. задачу 1967). Следовательно, OH=\frac{28}{9}
.
Источник: ЕГЭ. — 2017, 2 июня
