9591. В треугольной пирамиде PABC
с основанием ABC
известно, что AB=13
, PB=15
, \cos\angle PBA=\frac{48}{65}
. Основанием высоты этой пирамиды является точка C
. Прямые PA
и BC
перпендикулярны.
а) Докажите, что треугольник ABC
прямоугольный.
б) Найдите объём пирамиды PABC
.
Ответ. 90
.
Решение. а) Поскольку PC
— перпендикуляр к плоскости ABC
, сторона AC
основания пирамиды — ортогональная проекция наклонной PA
на эту плоскость, а так как PA\perp BC
, то по теореме о трёх перпендикулярах AC\perp BC
. Следовательно, треугольник ABC
прямоугольный с прямым углом при вершине C
.
б) По теореме косинусов
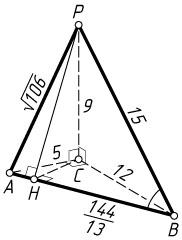
AP^{2}=PB^{2}+AB^{2}-2PB\cdot AB\cos\angle PBA=225+169-2\cdot15\cdot13\cdot\frac{48}{65}=106.
Пусть PH
— высота треугольника APB
. Из прямоугольного треугольника PHB
находим, что
BH=PB\cos\angle PBA=15\cdot\frac{48}{65}=\frac{144}{13}.
По теореме о трёх перпендикулярах CH
— высота прямоугольного треугольника ABC
, проведённая из вершины прямого угла. Значит,
BC=\sqrt{BH\cdot AB}=\sqrt{\frac{144}{13}\cdot13}=12
(см. задачу 2728).
По теореме Пифагора из прямоугольного треугольника ABC
находим, что AC=5
. Тогда
PC=\sqrt{AP^{2}-AC^{2}}=\sqrt{106-25}=\sqrt{81}=9.
Следовательно,
V_{PABC}=\frac{1}{3}S_{ABC}\cdot PC=\frac{1}{2}AC\cdot BC\cdot PC=\frac{1}{2}\cdot5\cdot12\cdot9=90.
Источник: ЕГЭ. — 2017

