9601. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A
, B
и C
, а на окружности другого основания — точка C_{1}
, причём CC_{1}
— образующая цилиндра, а отрезок AC
— диаметр основания. Известно, что AB=\sqrt{6}
, CC_{1}=2\sqrt{3}
, \angle ACB=30^{\circ}
.
а) Докажите, что угол между прямыми AC_{1}
и BC
равен 45^{\circ}
.
б) Найдите расстояние от точки B
до прямой AC_{1}
.
Ответ. \sqrt{5}
.
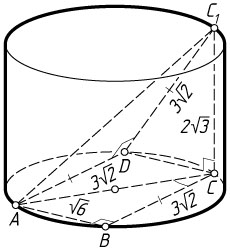
Решение. а) Точка B
лежит на окружности с диаметром AC
, поэтому \angle ABC=90^{\circ}
. Из прямоугольного треугольника ABC
находим, что
BC=AB\ctg30^{\circ}=\sqrt{6}\cdot\sqrt{3}=3\sqrt{2}.
Через точку A
проведём прямую, параллельную BC
. Пусть она пересекает окружность основания в точке D
. Значит, угол между скрещивающимися прямыми AC_{1}
и BC
равен углу между пересекающимися прямыми AC_{1}
и AD
. Четырёхугольник ABCD
— прямоугольник, поэтому AD=BC=3\sqrt{2}
.
Из прямоугольного треугольника DCC_{1}
находим, что
C_{1}D=\sqrt{CD^{2}+CC_{1}^{2}}=\sqrt{6+12}=\sqrt{18}=3\sqrt{2}=AD.
Отрезок CD
— ортогональная проекция наклонной C_{1}D
на плоскость основания цилиндра, причём CD\perp AD
. Значит, по теореме о трёх перпендикулярах C_{1}D\perp AD
, а равнобедренный треугольник ADC_{1}
— прямоугольный. Следовательно, угол между прямыми AC_{1}
и BC
равен углу DAC_{1}
, равному 45^{\circ}
.
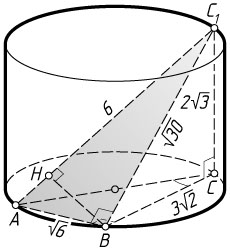
б) Отрезок BC
— ортогональная проекция наклонной C_{1}B
на плоскость ABC
. При этом BC\perp AB
. Значит, по теореме о трёх перпендикулярах CB_{1}\perp AB
, т. е. треугольник ABC_{1}
прямоугольный. Расстояние от точки B
до прямой AC_{1}
равно высоте BH
этого треугольника, проведённой из вершины прямого угла. По теореме Пифагора
BC_{1}=\sqrt{CC_{1}^{2}+BC^{2}}=\sqrt{12+18}=\sqrt{30},
а так как
AC_{1}=AD\sqrt{2}=3\sqrt{2}\cdot\sqrt{2}=6,
то
BH=\frac{AB\cdot BC_{1}}{AC_{1}}=\frac{\sqrt{6}\cdot\sqrt{30}}{6}=\sqrt{5}
(см. задачу 1967).
Источник: ЕГЭ. — 2018, 1 июня

