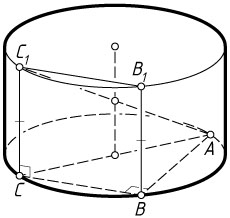
9602. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A
и B
, а на окружности другого основания — точки B_{1}
и C_{1}
, причём BB_{1}
— образующая цилиндра, а отрезок AC_{1}
пересекает ось цилиндра.
а) Докажите, что прямые AB
и B_{1}C_{1}
перпендикулярны.
б) Найдите расстояние между прямыми AC_{1}
и BB_{1}
, если AB=12
, B_{1}C_{1}=9
.
Ответ. 7{,}2
.
Решение. а) Пусть C
— точка на окружности того основания цилиндра, которое содержит A
и B
, а CC_{1}
— образующая цилиндра. Поскольку прямая AC_{1}
пересекает ось цилиндра, отрезок AC
— диаметр этого основания. Кроме того, BCC_{1}B_{1}
— прямоугольник, поэтому B_{1}C_{1}\parallel BC
. Точка B
лежит на окружности с диаметром AC
, значит, AB\perp BC
. Следовательно, AB\perp B_{1}C_{1}
.
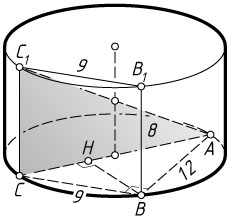
б) Пусть BH
— высота прямоугольного треугольника ABC
. Тогда BH\perp AC
и BH\perp CC_{1}
, значит, BH
— перпендикуляр к плоскости ACC_{1}
, параллельной прямой BB_{1}
и содержащей прямую AC_{1}
. Следовательно, расстояние между скрещивающимися прямыми AC_{1}
и BB_{1}
равно длине отрезка BH
.
Из прямоугольного треугольника ABC
находим, что
AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{AB^{2}+B_{1}C_{1}^{2}}=\sqrt{144+81}=15.
Следовательно (см. задачу 1967),
BH=\frac{AB\cdot BC}{AC}=\frac{12\cdot9}{15}=\frac{36}{5}=7{,}2.
Источник: ЕГЭ. — 2018, 1 июня

