9640. Дан куб ABCDA_{1}B_{1}C_{1}D_{1}
с ребром a
. Найдите радиус сферы, проходящей через вершины A
, C_{1}
и середины рёбер AA_{1}
и BB_{1}
.
Ответ. \frac{a\sqrt{14}}{4}
.
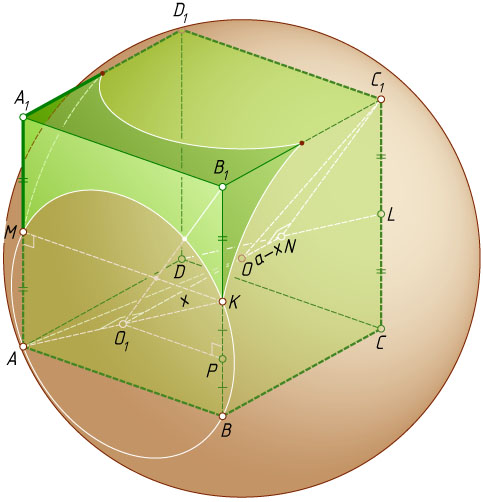
Решение. Пусть M
и K
— середины рёбер AA_{1}
и BB_{1}
соответственно. Центр O
сферы, проходящей через точки A
, M
и K
, лежит на прямой, проходящей через центр O_{1}
описанной окружности треугольника AMK
перпендикулярно плоскости AMK
(см. задачу 9056), т. е. плоскости грани AA_{1}B_{1}B
куба. Треугольник AMK
прямоугольный, поэтому O_{1}
— середина его гипотенузы AK
.
Пусть R
— искомый радиус, R_{1}
— радиус описанной окружности треугольника AMK
, L
— середина ребра CC_{1}
, N
— точка пересечения прямой OO_{1}
с гранью CC_{1}D_{1}D
(т. е. середина DL
), P
— проекция точки O_{1}
на прямую BB_{1}
(т. е. середина отрезка BK
).
Обозначим OO_{1}=x
. Из прямоугольных треугольников AMK
, AO_{1}O
, O_{1}PB_{1}
и C_{1}NO
находим, что
AK=\sqrt{MK^{2}+AM^{2}}=\sqrt{AB^{2}+AM^{2}}=\sqrt{a^{2}+\frac{a^{2}}{4}}=\frac{a\sqrt{5}}{2},
R^{2}=OA^{2}=OO_{1}^{2}+AO_{1}^{2}=x^{2}+\left(\frac{a\sqrt{5}}{4}\right)^{2}=x^{2}+\frac{5a^{2}}{16},
NC_{1}^{2}=O_{1}B_{1}^{2}=O_{1}P^{2}+B_{1}P^{2}=\left(\frac{a}{2}\right)^{2}+\left(\frac{3a}{4}\right)^{2}=\frac{a^{2}}{4}+\frac{9a^{2}}{16}=\frac{13a^{2}}{16},
R^{2}=OC_{1}^{2}=NC_{1}^{2}+ON^{2}=O_{1}B_{1}^{2}+(O_{1}N-OO_{1})^{2}=\frac{13a^{2}}{16}+(a-x)^{2}.
Из уравнения x^{2}+\frac{5a^{2}}{16}=\frac{13a^{2}}{16}+(a-x)^{2}
находим что x=\frac{3}{4}a
. Следовательно,
R=\sqrt{x^{2}+\frac{5a^{2}}{16}}=\sqrt{\frac{9a^{2}}{16}+\frac{5a^{2}}{16}}=\frac{a\sqrt{14}}{4}.
Источник: Шарыгин И. Ф. Геометрия. Стереометрия: Задачник для 10—11 кл. — М.: Дрофа, 1998. — № 44, с. 9
