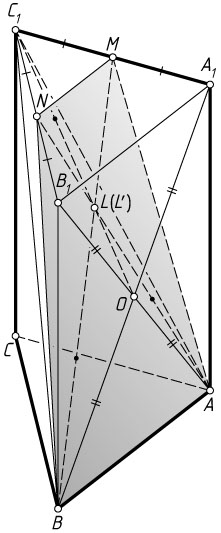
9730. В правильной треугольной призме ABCA_{1}B_{1}C_{1}
сторона основания равна 2, боковое ребро AA_{1}
равно 6, M
— середина ребра A_{1}C_{1}
, O
— точка пересечения диагоналей грани ABB_{1}A_{1}
.
а) Докажите, что точка пересечения прямой OC_{1}
с четырёхугольником, являющимся сечением призмы плоскостью ABM
, совпадает с точкой пересечения диагоналей этого четырёхугольника.
б) Найдите угол между прямой OC_{1}
и плоскостью ABM
.
Ответ. \arcsin\frac{3\sqrt{3}}{14}=\arccos\frac{13}{14}
Решение. а) Плоскость сечения проходит через прямую AB
, параллельную плоскости A_{1}B_{1}C_{1}
, и имеет с этой плоскостью общую точку M
, значит, эти плоскости пересекаются по прямой, проходящей через точку M
параллельно A_{1}B_{1}
(см. задачу 8003). Следовательно, рассматриваемое сечение — равнобокая трапеция ABNM
, где MN
— средняя линия треугольника A_{1}B_{1}C_{1}
.
Пусть медианы C_{1}O
и BM
треугольника BA_{1}C_{1}
пересекаются в некоторой точке L
. Тогда OL:LC_{1}=1:2
. Пусть медианы C_{1}O
и AN
треугольника AB_{1}C_{1}
пересекаются в некоторой точке L'
. Тогда OL':L'C_{1}=1:2
. Значит, точка L'
совпадает с L
. Следовательно, прямые BM
, AN
и OC_{1}
пересекаются в точке L
.
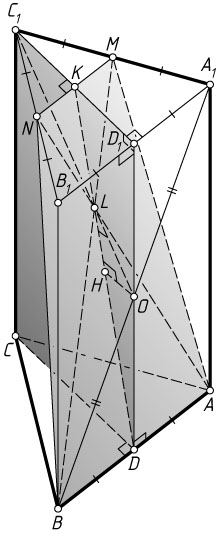
б) Пусть D
и D_{1}
— середины рёбер AB
и A_{1}B_{1}
соответственно, а K
— точка пересечения C_{1}D_{1}
и MN
. Тогда K
— середина отрезка MN
.
Опустим перпендикуляр OH
на прямую KD
. Тогда прямая OH
перпендикулярна двум пересекающимся прямым KD
и AB
плоскости ABM
. Значит, OH
— перпендикуляр к плоскости ABM
, LH
— ортогональная проекция наклонной OL
к этой плоскости, а искомый угол между прямой OC_{1}
и плоскостью ABM
— это угол OLH
.
Из равностороннего треугольника A_{1}B_{1}C_{1}
и прямоугольного треугольника DD_{1}K
находим, что
D_{1}K=\frac{1}{2}\cdot\frac{A_{1}B_{1}\sqrt{3}}{2}=\frac{\sqrt{3}}{2},
DK=\sqrt{DD_{1}^{2}+D_{1}K^{2}}=\sqrt{6^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}}=\sqrt{36+\frac{3}{4}}=\frac{7\sqrt{3}}{2}.
Прямоугольные треугольники ODH
и KDD_{1}
подобны, поэтому \frac{OH}{OD}=\frac{D_{1}K}{DK}
, откуда
OH=\frac{OD\cdot D_{1}K}{DK}=\frac{3\cdot\frac{\sqrt{3}}{2}}{\frac{7\sqrt{3}}{2}}=\frac{3}{7}.
Из прямоугольного треугольника C_{1}OD_{1}
находим, что
OC_{1}=\sqrt{OD_{1}^{2}+C_{1}D_{1}^{2}}=\sqrt{9+3}=2\sqrt{3}.
Тогда
OL=\frac{1}{3}OC_{1}=\frac{2\sqrt{3}}{3}.
Следовательно,
\sin\angle OLH=\frac{OH}{OL}=\frac{\frac{3}{7}}{\frac{2\sqrt{3}}{3}}=\frac{3\sqrt{3}}{14}.
Источник: ЕГЭ. — 2019, 24 июня, резервный день, задача 14

