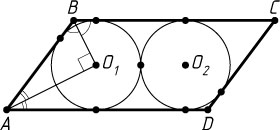
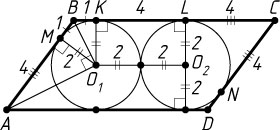
5240. В параллелограмме лежат две окружности, касающиеся друг друга и трёх сторон параллелограмма каждая.
а) Докажите, что одна из сторон параллелограмма видна из центра одной из окружностей под прямым углом.
б) Найдите площадь параллелограмма, если известно, что радиус одной из окружностей равен 2, а один из отрезков стороны параллелограмма от вершины до точки касания с одной из окружностей равен 4.
Ответ. 36.
Указание. Найдите отрезки, на которые точка касания одной из окружностей делит меньшую сторону параллелограмма.
Решение. а) Пусть окружность с центром O_{1}
касается сторон AD
, AB
и BC
параллелограмма ABCD
, а окружность с центром O_{2}
— сторон AD
, CD
и BC
. Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому AO_{1}
и BO_{1}
— биссектрисы углов, сумма которых равна 180^{\circ}
. Следовательно, эти биссектрисы пересекаются под прямым углом, т. е. \angle AO_{1}B=90^{\circ}
. Что и требовалось доказать.
б) Каждая из окружностей касается параллельных прямых AD
и BC
, значит, окружности равны. Расстояние между точками их касания с большей стороной параллелограмма равно сумме их радиусов, т. е. 4. Пусть окружность с центром O_{1}
касается стороны AB
в точке M
, стороны BC
— в точке K
, а AM=4
. Поскольку радиус O_{1}M
— высота прямоугольного треугольника AO_{1}B
, проведённая из вершины прямого угла (см. задачи 313, 656), то
BK=BM=\frac{O_{1}M^{2}}{AM}=\frac{4}{4}=1.
Если окружность с центром O_{2}
касается сторон CD
и BC
в точках N
и L
соответственно, то CL=CN=AM=4
. Тогда BC=1+4+4=9
, а так как высота параллелограмма, опущенная на сторону BC
, равна диаметру окружности, т. е. 4, то S_{ABCD}=9\cdot4=36
.