44. В трапеции ABCD
основание AD
вдвое больше основания BC
, угол A
равен 45^{\circ}
, угол D
равен 60^{\circ}
. На диагоналях трапеции как на диаметрах построены окружности, пересекающиеся в точках M
и N
. Хорда MN
пересекает основание AD
в точке E
. Найдите отношение AE:ED
.
Ответ. \sqrt{3}
.
Указание. 1. Основания высот трапеции, опущенных из вершин B
и C
, лежат на указанных окружностях.
2. Пусть продолжения боковых сторон AB
и CD
трапеции ABCD
пересекаются в точке T
. Тогда TE
— высота треугольника ATD
.
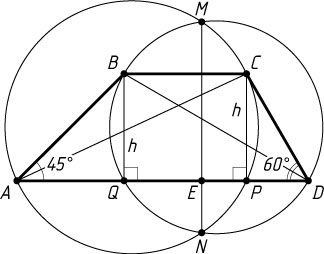
Решение. Первый способ. Пусть окружность с диаметром BD
пересекает основание AD
трапеции ABCD
в точке Q
, а окружность с диаметром AC
— в точке P
. Тогда CP
и BQ
— высоты трапеции.
Обозначим CP=BQ=h
. Тогда DP=\frac{h}{\sqrt{3}}
, AQ=h
. По теореме о произведениях отрезков пересекающихся хорд
DE\cdot EQ=NE\cdot EM=AE\cdot EP,~\mbox{или}~\left(\frac{h}{\sqrt{3}}+PE\right)EQ=(h+QE)PE.
Отсюда находим, что PE=\frac{EQ}{\sqrt{3}}
. Следовательно,
\frac{DE}{AE}=\frac{DP+PE}{AQ+QE}=\frac{\frac{h}{\sqrt{3}}+\frac{EQ}{\sqrt{3}}}{h+QE}=\frac{1}{\sqrt{3}}.
Второй способ. Пусть продолжения боковых сторон AB
и CD
трапеции ABCD
пересекаются в точке T
. Поскольку прямая MN
— радикальная ось окружностей с диаметрами AC
и BD
(см. задачу 6392), то на ней лежит ортоцентр треугольника ATD
(см. задачу 6011), а так как общая хорда двух пересекающихся окружностей перпендикулярна их линии центров, точки T
, M
, N
, E
и H
лежат на одной прямой. Значит, TE
— высота треугольника ATD
. Поэтому
DE=TE\ctg\angle ADC=TE\ctg60^{\circ}=\frac{TE}{\sqrt{3}},~AE=TE\ctg45^{\circ}=TE.
Следовательно,
\frac{DE}{AE}=\frac{\frac{TE}{\sqrt{3}}}{TE}=\frac{1}{\sqrt{3}}.
Примечание. Условие AD=2BC
— лишнее.
Источник: Вступительный экзамен на физический факультет МГУ. — 1972, вариант 2, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 189
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.34, с. 96
