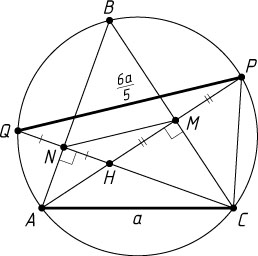
78. Продолжения высот AM
и CN
остроугольного треугольника ABC
пересекают описанную около него окружность в точках P
и Q
. Найдите радиус описанной окружности, если AC=a
, PQ=\frac{6a}{5}
.
Ответ. \frac{5a}{8}
.
Указание. Точка, симметричная ортоцентру треугольника относительно стороны, лежит на описанной окружности треугольника (см. задачу 4785). Треугольник BMN
подобен треугольнику BAC
, причём коэффициент подобия равен |\cos\angle ABC|
(см. задачу 19).
Решение. Пусть H
— точка пересечения высот. Известно, что точка, симметричная ортоцентру треугольника относительно стороны, лежит на описанной окружности треугольника (см. задачу 4785). Поэтому HM=MP
и HN=NQ
. Значит, MN
— средняя линия треугольника HQP
. Следовательно,
MN=\frac{1}{2}PQ=\frac{3a}{5}.
Треугольник BMN
подобен треугольнику BAC
, причём коэффициент подобия равен \cos\angle ABC
(см. задачу 19). Значит,
\cos\angle ABC=\frac{MN}{AC}=\frac{\frac{3}{5}a}{a}=\frac{3}{5},~\sin\angle ABC=\frac{4}{5}.
Если R
— искомый радиус, то
R=\frac{AC}{2\sin\angle ABC}=\frac{a}{2\cdot\frac{4}{5}}=\frac{5a}{8}.
Источник: Вступительный экзамен в МФТИ. — 1979, билет 4, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 79-4-4, с. 214
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.19, с. 123
