150. Для данной хорды MN
окружности рассматриваются треугольники ABC
, основаниями которых являются диаметры AB
этой окружности, не пересекающие MN
, а стороны AC
и BC
проходят через концы M
и N
хорды MN
. Докажите, что высоты всех таких треугольников ABC
, опущенные из вершины C
на сторону AB
, пересекаются в одной точке.
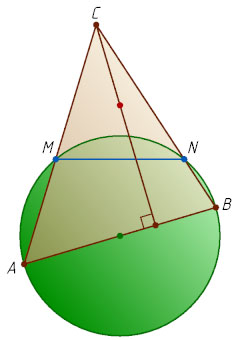
Указание. Точки M
, N
, C
и точка пересечения высот треугольника ABC
лежат на одной окружности. Её центр — искомая точка.
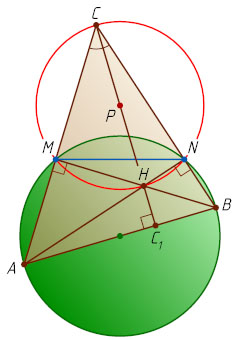
Решение. AN
и BM
— также высоты треугольника ABC
. Пусть H
— их точка пересечения. Точки M
, C
, N
, H
лежат на окружности с диаметром CH
. Пусть P
— её центр.
Поскольку высоты треугольника пересекаются в одной точке, высота CC_{1}
треугольника ABC
проходит через точку P
.
Угол C
не зависит от положения диаметра AB
, так как
\angle C=\frac{\smile AB-\smile MN}{2}=\frac{180^{\circ}-\smile MN}{2}
(см. задачу 27). Поэтому любому указанному в условии положению диаметра AB
соответствует одна и та же окружность с центром P
. Следовательно, высоты CC_{1}
всех таких треугольников ABC
проходят через точку P
.
Примечание. См. также задачу 12492.
Автор: Куланин Е. Д.
Источник: Турнир городов. — 1990/91
Источник: Журнал «Квант». — 1991, № 9, с. 22, М1276
Источник: Задачник «Кванта». — М1276

